
 的⊙O內有互相垂直的兩條弦AB、CD相交于P點.
的⊙O內有互相垂直的兩條弦AB、CD相交于P點.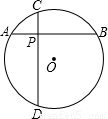
 解:(1)連接AD,BC,
解:(1)連接AD,BC,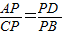 ,
, )2-42=4,ON2=(2
)2-42=4,ON2=(2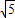 )2-32=11,
)2-32=11,
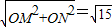 .
. )2成立,知道這三個量中的任意兩個,就可以求出另外一個.
)2成立,知道這三個量中的任意兩個,就可以求出另外一個. 

科目:初中數學 來源: 題型:
 如圖,半徑為30km 的圓A是環保部分劃定的生態保護區,B、C是位于保護區附近相距100km的兩城市.如果在 B、C兩城之間修一條筆直的公路,經測量∠ABC=45°,∠ACB=30°.
如圖,半徑為30km 的圓A是環保部分劃定的生態保護區,B、C是位于保護區附近相距100km的兩城市.如果在 B、C兩城之間修一條筆直的公路,經測量∠ABC=45°,∠ACB=30°.查看答案和解析>>
科目:初中數學 來源: 題型:
 (2013•高淳縣一模)如圖,半徑為2的兩個等圓⊙O1與⊙O2外切于點P,過O1作⊙O2的兩條切線,切點分別為A、B,與⊙O1分別交于C、D,則弧APB與弧CPD的長度之和為
(2013•高淳縣一模)如圖,半徑為2的兩個等圓⊙O1與⊙O2外切于點P,過O1作⊙O2的兩條切線,切點分別為A、B,與⊙O1分別交于C、D,則弧APB與弧CPD的長度之和為查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com