Question

閱讀理解
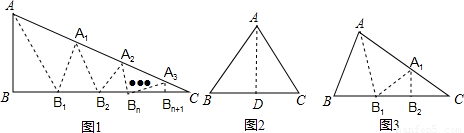
如圖1，△ABC中，沿∠BAC的平分線AB₁折疊，剪掉重疊部分；將余下部分沿∠B₁A₁C的平分線A₁B₂折疊，剪掉重疊部分；將余下部分沿∠B_nA_nC的平分線A_nB_n+1折疊，點B_n與點C重合．無論折疊多少次，只要最后一次恰好重合，我們就稱∠BAC是△ABC的好角．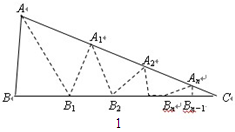

小麗展示了確定∠BAC是△ABC的好角的兩種情形．
情形一：如圖2，沿等腰三角形ABC頂角∠BAC的平分線AB₁折疊，點B與點C重合；

情形二：如圖3，沿 △ABC的∠BAC的平分線AB₁折疊，剪掉重疊部分；
將余下的部分沿∠B₁A₁C的平分線 A₁B₂折疊，此時點B₁與點C重合．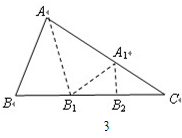
 
探究發現
（1）△ABC中，∠B=2∠C，經過兩次折疊，∠BAC  （填“是”或“不是”）△ABC的好角；
（2）若經過三次折疊發現∠BAC是△ABC的好角，請探究∠B與∠C之間的等量關系（不妨設∠B>∠C）．
根據以上內容猜想：若經過n次折疊∠BAC是△ABC的好角，則∠B與∠C之問的等量關系為      ．（不妨設∠B>∠C）
應用提升：
（3）小麗找到一個三角形，三個角分別為15º，60º，l05º，發現60º和l05º的兩個角都是此三角形的好角．
請你完成，如果一個三角形的最小角是4º，試求出三角形另外兩個角的度數，使該三角形的三個角均是此三角形的好角．

Answer 1

（1）是；（2）∠B=n∠C；（3）4º，172º；8º，168º；16º，160º；44º，132º；88º，88º．

解析試題分析：（1）仔細分析題意根據折疊的性質及“好角”的定義即可作出判斷；
（2）因為經過三次折疊∠BAC是△ABC的好角，所以第三次折疊的∠A₂B₂C=∠C，由∠ABB₁=∠AA₁B₁，∠AA₁B₁=∠A₁B₁C+∠C，又∠A₁B₁C=∠A₁A₂B₂，∠A₁A₂B₂=∠A₂B₂C+∠C，∠ABB₁=∠A₁B₁C+∠C=∠A₂B₂C+∠C+∠C=3∠C，由此即可求得結果；
（3）因為最小角是4º是△ABC的好角，根據好角定義，則可設另兩角分別為4mº，4mnº（其中m、n都是正整數），由題意得4m+4mn+4=180，所以m(n+1)=44，再根據m、n都是正整數可得 m與n+1是44的整數因子，從而可以求得結果．
（1）由題意得∠BAC是△ABC的好角；
（2）因為經過三次折疊∠BAC是△ABC的好角，所以第三次折疊的∠A₂B₂C=∠C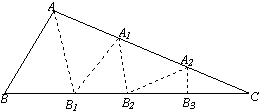

因為∠ABB₁=∠AA₁B₁，∠AA₁B₁=∠A₁B₁C+∠C，又∠A₁B₁C=∠A₁A₂B₂，∠A₁A₂B₂=∠A₂B₂C+∠C，
所以∠ABB₁=∠A₁B₁C+∠C=∠A₂B₂C+∠C+∠C=3∠C
由此可猜想若經過n次折疊∠BAC是△ABC的好角，則∠B=n∠C；
（3）因為最小角是4º是△ABC的好角，
根據好角定義，則可設另兩角分別為4mº，4mnº（其中m、n都是正整數）．
由題意，得4m+4mn+4=180，所以m(n+1)=44．
因為m、n都是正整數，所以m與n+1是44的整數因子，
因此有：m=1，n+1=44；m=2，n+1=22；m=4，n+1=11；m=11，n+1=4；m=22，n+1=2．
所以m=1，n=43；m=2，n=21；m=4，n=10；m=11，n=3；m=22，n=1．
所以4m=4，4mn=172；4m=8，4mn=168；4m=16，4mn=160；4m=44，4mn=132；4m=88，4mn=88．
所以該三角形的另外兩個角的度數分別為：4º，172º；8º，168º；16º，160º；44º，132º；88º，88º．
考點：折疊問題的綜合題
點評：此類問題是初中數學的重點和難點，在中考中極為常見，一般以壓軸題形式出現，難度較大.