
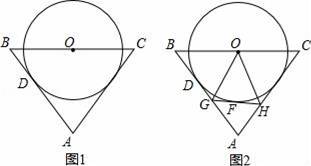
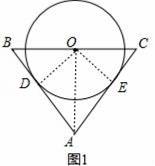
如圖1,△ABC中,AB=AC,點O是BC的中點,以O為圓心的⊙O與AB邊相切于點D.
(1)判斷AC邊與⊙O的位置關系,說明理由;
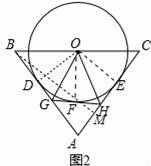
(2)如圖2,若AB=5,BC=6,點F為⊙O上一動點,過點F作⊙O的切線分別交AD邊、AC邊于點G、H,連結OG、OH.
①設∠BAC=α,則∠GOH= (用含α的代數式表示);
②若△OGH是以GH為腰的等腰三角形,求BG的長.

【考點】圓的綜合題.
【專題】綜合題.
【分析】(1)作OE⊥AC于E,連結OA、OD,如圖1,先利用切線的性質得OD⊥AB,再根據等腰三角形的性質,由AB=AC,點O是BC的中點得到AO平分∠BAC,則利用角平分線的性質得到OE=OD,于是可根據切線的判定方法得到AC為⊙O的切線;
(2)①作OE⊥AC于E,BM⊥AC于M,連結OF、OD,如圖2,由切線的性質得OF⊥GH,由切線長定理得GD=GF,HF=HE,于是可根據角平分線定理的逆定理得∠DOG=∠FOG,∠EOH=∠FOH,則∠GOH=
 ∠DOE,再由四邊形內角和得到∠DOE+∠A=180°,所以∠GOEH=90°﹣
∠DOE,再由四邊形內角和得到∠DOE+∠A=180°,所以∠GOEH=90°﹣
 α;
α;
②在圖1中,AB=5,OB=OC=
 BC=3,利用勾股定理和面積法先計算出OA=5,OD=
BC=3,利用勾股定理和面積法先計算出OA=5,OD=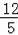
 ,BD=
,BD=
 ,BM=
,BM=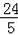
 ,AM=
,AM=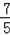
 ,接著分類討論:當GH=GO時,∠GHO=∠GOH=90°﹣
,接著分類討論:當GH=GO時,∠GHO=∠GOH=90°﹣
 α,則∠OGH=α,于是可判斷Rt△OGF∽Rt△BAM,利用相似比可計算出GF=
α,則∠OGH=α,于是可判斷Rt△OGF∽Rt△BAM,利用相似比可計算出GF=
 ,則DG=GF=
,則DG=GF=
 ,所以BG=BD+DG=
,所以BG=BD+DG=
 ;當GH=OH時,同樣可證明Rt△OHF∽Rt△BAM,利用相似比可計算出FH=
;當GH=OH時,同樣可證明Rt△OHF∽Rt△BAM,利用相似比可計算出FH=
 ,OH=
,OH=
 ,則GH=OH=
,則GH=OH=
 ,所以GF=GH﹣FH=
,所以GF=GH﹣FH=
 =DG,則BG=BD+DG=
=DG,則BG=BD+DG=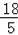
 .
.
【解答】解:(1)AC邊與⊙O相切.理由如下:
作OE⊥AC于E,連結OA、OD,如圖1,
∵以O為圓心的⊙O與AB邊相切于點D,
∴OD⊥AB,
∵AB=AC,點O是BC的中點,
∴AO平分∠BAC,
∴OE=OD,
∴AC為⊙O的切線;
(2)①作OE⊥AC于E,BM⊥AC于M,連結OF、OD,如圖2,
∵GH為⊙O的切線,
∴OF⊥GH,
∵AB和AC為⊙O的切線,
∴GD=GF,HF=HE,
∴∠DOG=∠FOG,∠EOH=∠FOH,
∴∠GOH=
 ∠DOE,
∠DOE,
∵∠DOE+∠A=180°,
∴∠GOEH=
 (180°﹣α)=90°﹣
(180°﹣α)=90°﹣
 α,
α,
故答案為90°﹣
 α;
α;
②在圖1中,AB=5,OB=OC=
 BC=3,則OA=
BC=3,則OA=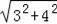
 =5,
=5,
∵
 OD•AB=
OD•AB=
 OB•OA,
OB•OA,
∴OD=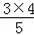
 =
=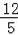
 ,
,
在Rt△BOD中,BD=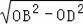
 =
=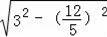
 =
=
 ,
,
在圖2中,
∵
 BM•AC=
BM•AC=
 BC•OA,
BC•OA,
∴BM=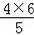
 =
=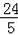
 ,
,
在Rt△ABM中,AM=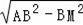
 =
=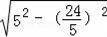
 =
=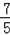
 ,
,
當GH=GO時,∠GHO=∠GOH=90°﹣
 α,
α,
∴∠OGH=180°﹣2(90°﹣
 α)=α,
α)=α,
∴Rt△OGF∽Rt△BAM,
∴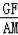
 =
=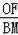
 ,即
,即
 =
=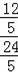
 ,解得GF=
,解得GF=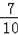
 ,
,
∴DG=GF=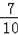
 ,
,
∴BG=BD+DG=
 +
+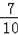
 =
=
 ;
;
當GH=OH時,∠GHO=∠GOH=90°﹣
 α,則∠OHG=α,
α,則∠OHG=α,
∴Rt△OHF∽Rt△BAM,
∴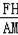
 =
=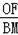
 =
=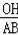
 ,即
,即
 =
=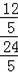
 =
=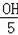
 ,解得FH=
,解得FH=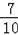
 ,OH=
,OH=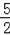

∴GH=OH=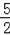
 ,
,
∴GF=GH﹣FH=
 ﹣
﹣
 =
=
 ,
,
∴DG=GF=
 ,
,
∴BG=BD+DG=
 +
+
 =
=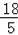
 ,
,
綜上所述,BG的長為
 或
或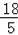
 .
.


【點評】本題考查了圓的綜合題:熟練掌握圓的切線的判定與性質、切線長定理和等腰三角形的性質;會利用相似比和勾股定理計算線段的長;會運用分類討論的思想解決數學問題.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
小偉擲一枚質地均勻的骰子,骰子的六個面上分別刻有1到6的點數,下列事件是隨機事件的是( )
A.擲一次骰子,在骰子向上的一面上的點數大于0
B.擲一次骰子,在骰子向上的一面上的點數為7
C.擲三次骰子,在骰子向上的一面上的點數之和剛好為18
D.擲兩次骰子,在骰子向上的一面上的點數之積剛好是11
查看答案和解析>>
科目:初中數學 來源: 題型:
“搶紅包”是2015年春節十分火爆的一項網絡活動,某企業有4000名職工,從中隨機抽取350人,按年齡分布和對“搶紅包”所持態度情況進行了調查,并將調查結果繪成了條形統計圖和扇形統計圖.


(1)這次調查中,如果職工年齡的中位數是整數,那么這個中位數所在的年齡段是哪一段?
(2)如果把對“搶紅包”所持態度中的“經常(搶紅包)”和“偶爾(搶紅包)”統稱為“參與搶紅包”,那么這次接受調查的職工中“參與搶紅包”的人數是多少?
(3)請估計該企業“從不(搶紅包)”的人數是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
如圖,已知反比例函數y=
 與一次函數y=x+b的圖象在第一象限相交于點A(1,﹣k+4).
與一次函數y=x+b的圖象在第一象限相交于點A(1,﹣k+4).
(1)試確定這兩個函數的表達式;
(2)求出這兩個函數圖象的另一個交點B的坐標,并求△AOB的面積.


查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com