
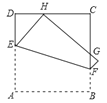
【題目】如圖,將正方形ABCD折疊,使點A與CD邊上的點H重合(H不與C,D重合),折痕交AD于點E,交BC于點F,邊AB折疊后與邊BC交于點G.設正方形ABCD周長為m,△CHG周長為n,則![]() 的值為( )
的值為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
由題意連接AH、AG,作AM⊥HG于M.利用正方形的性質以及全等三角形的判定與性質進行等量替換從而求出![]() 的值.
的值.
解:連接AH、AG,作AM⊥HG于M.
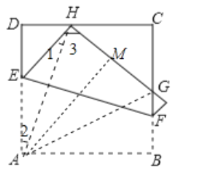
∵四邊形ABCD是正方形,
∴AD=AB.
∴AM=AB.
∵EA=EH,
∴∠1=∠2,
∵∠EAB=∠EHG=90°,
∴∠HAB=∠AHG,
∵DH∥AB,
∴∠DHA=∠HAB=∠AHM,
∵AH=AH,∠D=∠AMH=90°,
∴△AHD≌△AHM,
∴DH=HM,AD=AM,
∵AM=AB,AG=AG,
∴Rt△AGM≌Rt△AGB,
∴GM=GB,
∴△GCH的周長=n=CH+HM+MG+CG=CH+DH+CG+GB=2BC,
∵四邊形ABCD的周長=m=4BC,
∴![]() .
.
故選:B.


 芝麻開花課程新體驗系列答案
芝麻開花課程新體驗系列答案 怎樣學好牛津英語系列答案
怎樣學好牛津英語系列答案科目:初中數學 來源: 題型:
【題目】經過某十字路口的汽車,它可能繼續直行,也可能向左轉或向右轉,如果這三種可能性大小相同,現有兩輛汽車經過這個十字路口.
(1)試用樹狀圖或列表法中的一種列舉出這兩中的一種列舉出這輛汽車行駛方向所有可能的結果;
(2)求至少有一輛汽車向左轉的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某公司擬用運營指數y來量化考核司機的工作業績,運營指數(y)與運輸次數(n)和平均速度(x)之間滿足關系式為y=ax2+bnx+100,當n=1,x=30時,y=190;當n=2,x=40時,y=420
用含x和n的式子表示y;
當運輸次數定為3次,求獲得最大運營指數時的平均速度;
若n=2,x=40,能否在n增加m%(m>0),同時x減少m%的情況下,而y的值保持不變,若能,求出m的值;若不能,請說明理由.
參考公式:拋物線y=ax2+bx+c(a≠0)的頂點坐標是(-![]() ,
,![]() )
)
查看答案和解析>>
科目:初中數學 來源: 題型:
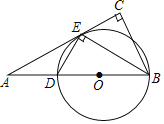
【題目】如圖,在Rt△ABC中,∠C=90°,BE平分∠ABC交AC于點E,作ED⊥EB交AB于點D,⊙O是△BED的外接圓.
(1)求證:AC是⊙O的切線;
(2)已知⊙O的半徑為2.5,BE=4,求BC,AD的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在正方形ABCD中,點P是CD上一動點,連結PA,分別過點B、D作BE⊥PA、DF⊥PA,垂足為E、F,如圖①.
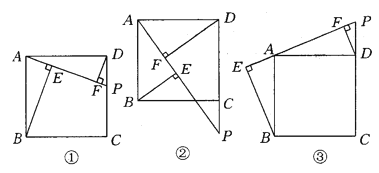
(1)請探索BE、DF、EF這三條線段長度具有怎樣的數量關系,若點P在DC的延長線上(如圖②),那么這三條線段的長度之間又有怎樣的數量關系?若點P在CD的延長線上呢(如圖③)?請分別直接寫出結論.
(2)請在(1)中的三個結論中選擇一個加以證明.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為鼓勵大學畢業生自主創業,某市政府出臺了相關政策:由政府協調,本市企業按成本價提供產品給大學畢業生自主銷售,成本價與出廠價之間的差價由政府承擔.李明按照相關政策投資銷售本市生產的一種新型節能燈.已知這種節能燈的成本價為每件![]() 元,出廠價為每件
元,出廠價為每件![]() 元,每月銷售量
元,每月銷售量![]() (件)與銷售單價
(件)與銷售單價![]() (元)之間的關系近似滿足一次函數:
(元)之間的關系近似滿足一次函數:![]() .
.
(1)李明在開始創業的第一個月將銷售單價定為![]() 元,那么政府這個月為他承擔的總差價為多少元?
元,那么政府這個月為他承擔的總差價為多少元?
(2)設李明獲得的利潤為![]() (元),當銷售單價定為多少元時,每月可獲得最大利潤?
(元),當銷售單價定為多少元時,每月可獲得最大利潤?
(3)物價部門規定,這種節能燈的銷售單價不得高于![]() 元.如果李明想要每月獲得的利潤不低于
元.如果李明想要每月獲得的利潤不低于![]() 元,那么政府為他承擔的總差價最少為多少元?
元,那么政府為他承擔的總差價最少為多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某超市以20元/千克的進貨價購進了一批綠色食品,如果以30元/千克銷售這些綠色食品,那么每天可售出400千克.由銷售經驗可知,每天的銷售量y(千克)與銷售單價x(元)(x≥30)存在如圖所示的一次函數關系.
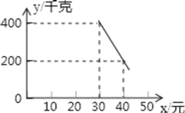
(1)試求出y與x的函數關系式;
(2)設該超市銷售該綠色食品每天獲得利潤w元,當銷售單價為何值時,每天可獲得最大利潤?最大利潤是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小李準備進行如下的操作,把一根長![]() 的鐵絲剪成兩段,并把每段首尾相連各圍成一個長寬不等的矩形,兩矩形相似且相似比為
的鐵絲剪成兩段,并把每段首尾相連各圍成一個長寬不等的矩形,兩矩形相似且相似比為![]() .
.
(1)要使這兩個矩形的面積之和為![]() ,較小矩形的長寬各是多少?
,較小矩形的長寬各是多少?
(2)小李認為這兩個矩形的面積和不可能為![]() ,你同意嗎?說明理由.(說明:相似多邊形的周長比等于相似比,面積比等于相似比的平方)
,你同意嗎?說明理由.(說明:相似多邊形的周長比等于相似比,面積比等于相似比的平方)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在直角坐標系中,矩形OABC的頂點O與坐標原點重合,A,C分別在y軸,x軸上,點B的坐標為![]() ,直線
,直線![]() 分別交AB,BC于點M,N,
分別交AB,BC于點M,N,![]() ,反比例函數
,反比例函數![]() 圖象經過點M,N.
圖象經過點M,N.
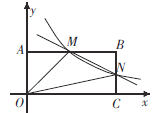
(1)求反比例函數的表達式;
(2)根據圖象,請直接寫出不等式![]() 的解集________.
的解集________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com