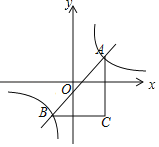
【題目】如圖，直線y=x+m與雙曲線y=
相交于A，B兩點，BC∥x軸，AC∥y軸，則△ABC面積的最小值為_____．
【答案】6
【解析】
根據雙曲線y=
過A，B兩點，可設A（a，
），B（b，
），則C（a，）．將y=x+m代入y=，整理得x2+mx-3=0，由于直線y=x+m與雙曲線y=相交于A，B兩點，所以a、b是方程x2+mx-3=0的兩個根，根據根與系數的關系得出a+b=-m，ab=-3，那么（a-b）2=（a+b）2-4ab=m2+12．再根據三角形的面積公式得出S△ABC=
ACBC=m2+6，利用二次函數的性質即可求出當m=0時，△ABC的面積有最小值6．
設A（a，），B（b，），則C（a，）．
將y=x+m代入y=，得x+m=，
整理，得x2+mx-3=0，
則a+b=-m，ab=-3，
∴（a-b）2=（a+b）2-4ab=m2+12．
∵S△ABC=ACBC
=（-）（a-b）
=
（a-b）
=（a-b）2
=（m2+12）
=m2+6，
∴當m=0時，△ABC的面積有最小值6．
故答案為6．
科目：初中數學 來源： 題型：
【題目】已知一次函數
的圖象過點（98，19），它與X軸的交點為（P，0），與y軸交點為（0，q），若p是質數，q是正整數，那么滿足條件的所有一次函數的個數為（ ）。
A.0B.1C.2D.大于2的整數
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，鈍角△ABC中，AB=AC，BC=2
，O是邊AB上一點，以O為圓心，OB為半徑作⊙O，交邊AB于點D，交邊BC于點E，過E作⊙O的切線交邊AC于點F．
（1）求證：EF⊥AC．
（2）連結DF，若∠ABC=30°，且DF∥BC，求⊙O的半徑長．
查看答案和解析>>
科目：初中數學 來源： 題型：
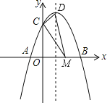
【題目】如圖，對稱軸為
的拋物線
與
軸交于
、
兩點，與
軸交于
點，其中點坐標為
設拋物線的頂點為
．
求拋物線的解析式及頂點坐標；
為軸上的一點，當
的周長最小時，求點
的坐標及的周長．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】中秋節前夕，某超市采購了一批土特產，根據以往銷售經驗，每天的售價與銷售量之間有如下表的關系：
每千克售價(元) | 38 | 37 | 36 | 35 | … | 20 |
每天銷售量(千克) | 50 | 52 | 54 | 56 | … | 86 |
設當售價從38元/千克下調到x元/千克時，銷售量為y千克．
(1)根據上述表格中提供的數據，通過在直角坐標系中描點連線等方法，猜測并求出y與x之間的函數解析式；
(2)如果這種土特產的成本價是20元/千克，為使某一天的利潤為780元，那么這一天每千克的售價應為多少元？(利潤＝銷售總金額－成本)
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】甲、乙兩家快遞公司攬件員（攬收快件的員工）的日工資方案如下：
甲公司為“基本工資+攬件提成”，其中基本工資為70元/日，每攬收一件提成2元；
乙公司無基本工資，僅以攬件提成計算工資．若當日攬件數不超過40，每件提成4元；若當日攪件數超過40，超過部分每件多提成2元．
如圖是今年四月份甲公司攬件員人均攬件數和乙公司攪件員人均攬件數的條形統計圖：
（1）現從今年四月份的30天中隨機抽取1天，求這一天甲公司攬件員人均攬件數超過40（不含40）的概率；
（2）根據以上信息，以今年四月份的數據為依據，并將各公司攬件員的人均攬件數視為該公司各攬件員的
攬件數，解決以下問題：
①估計甲公司各攬件員的日平均件數；
②小明擬到甲、乙兩家公司中的一家應聘攬件員，如果僅從工資收入的角度考慮，請利用所學的統計知識幫他選擇，井說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖1，直線AM⊥AN，AB平分∠MAN，過點B作BC⊥BA交AN于點C；動點E、D同時從A點出發，其中動點E以2cm/s的速度沿射線AN方向運動，動點D以1cm/s的速度運動；已知AC＝6cm，設動點D，E的運動時間為t．
（1）當點D在射線AM上運動時滿足S△ADB：S△BEC＝2：1，試求點D，E的運動時間t的值；
（2）當動點D在直線AM上運動，E在射線AN運動過程中，是否存在某個時間t，使得△ADB與△BEC全等？若存在，請求出時間t的值；若不存在，請說出理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，長方形ABCD中，點E是邊CD的中點，將△ADE沿AE折疊得到△AFE，且點F在長方形ABCD內．將AF延長交邊BC于點G．若BG=3CG，則
=（ ）
A.
B.1C.
D.
查看答案和解析>>
科目：初中數學 來源： 題型：
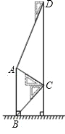
【題目】如圖，某中學在教學樓前新建了一座雕塑
．為了測量雕塑的高度，小明在二樓找到一點
，利用三角尺測得雕塑頂端點
的仰角為
，底部點
的俯角為
，小華在五樓找到一點
，利用三角尺測得點的俯角為
．若
為
，則雕塑的高度為________
．（結果精確到
，參考數據：
）．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com