(1)解:△BOM,△CON,△BOC,△AMN,△ABC均為等腰三角形,
所以,除△ABC外還有4個;
(2)證明:∵BO是∠ABC的平分線,
∴∠MBO=∠CBO,
∵MN∥BC,
∴∠CBO=∠MOB,
∴∠MBO=∠MOB,
∴△BMO是等腰三角形;
(3)證明:∵AB=AC,
∴∠ABC=∠ACB,
∵MN∥BC,
∴∠AMN=∠ABC,∠ANM=∠ACB,
∴∠AMN=∠ANM,
∴AM=AN,
∴AB-AM=AC-AN,
即BM=CN,
根據(2)△BMO是等腰三角形,
∴BM=OM,
同理可得CN=ON,
∴MN=OM+ON=BM+CN=2BM;
(4)解:結論不正確;
∵O為MN中點,
∴OM=ON,
又∵MN∥BC,
∴∠BMO=∠CNO,BM=CN,
在△BOM和△CON中,
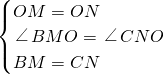
,
∴△BOM≌△CON(SAS),
∴∠OBM=∠OCN,
又∵AB=AC,
∴∠ABC=∠ACB,
∴∠OBC=∠OCB,
但不能肯定∠OBM=∠OBC,
即不能確定其為角平分線.
∴此問結論不正確.
分析:(1)寫出圖中的三角形都是等腰三角形;
(2)根據角平分線的定義可得∠MBO=∠CBO,再根據兩直線平行,內錯角相等可得∠CBO=∠MOB,從而得到∠MBO=∠MOB,即可得證;
(3)根據等邊對等角求出∠ABC=∠ACB,再根據兩直線平行,同位角相等求出∠AMN=∠ABC,∠ANM=∠ACB,然后求出∠AMN=∠ANM,再根據等角對等邊求出AM=AN,然后求出BM=CN,再根據(2)的結論可得BM=MO,CN=ON,從而得證;
(4)先求出△BOM和△CON全等,根據全等三角形對應角相等可得∠OBM=∠OCN,再求出∠OBC=∠OCB,再根據不能肯定∠OBM=∠OBC,從而得到此題結論不正確.
點評:本題考查了等腰三角形的判定與性質,全等三角形的判定與性質,角平分線的定義,平行線的性質,綜合性較強,但難度不大,仔細分析圖形是解題的關鍵.

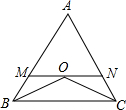 如圖,在△ABC中,AB=AC,∠B與∠C的角平分線交于點O,過O點作MN∥BC,分別交AB,AC于M,N.
如圖,在△ABC中,AB=AC,∠B與∠C的角平分線交于點O,過O點作MN∥BC,分別交AB,AC于M,N.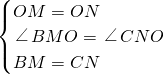 ,
,

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案 如圖,在△ABC中,∠ACB=90°,AC=BC=1,取斜邊的中點,向斜邊作垂線,畫出一個新的等腰三角形,如此繼續下去,直到所畫出的直角三角形的斜邊與△ABC的BC重疊,這時這個三角形的斜邊為
如圖,在△ABC中,∠ACB=90°,AC=BC=1,取斜邊的中點,向斜邊作垂線,畫出一個新的等腰三角形,如此繼續下去,直到所畫出的直角三角形的斜邊與△ABC的BC重疊,這時這個三角形的斜邊為