
 如圖,拋物線y=x2-3x+$\frac{5}{4}$與x軸相交A、B兩點,與y軸相交于點C,D是直線BC下方的拋物線上一點,過點D作y軸的平行線,與直線BC相交于點E.
如圖,拋物線y=x2-3x+$\frac{5}{4}$與x軸相交A、B兩點,與y軸相交于點C,D是直線BC下方的拋物線上一點,過點D作y軸的平行線,與直線BC相交于點E.分析 (1)求出B、C兩點坐標,利用待定系數法即可解決問題.
(2)設D坐標為(m,m2-3m+$\frac{5}{4}$),則點E坐標為(m,-$\frac{1}{2}$m+$\frac{5}{4}$),設DE的長為d,構建二次函數,利用二次函數的性質即可解決問題.
解答 解:(1)對于拋物線y=x2-3x+$\frac{5}{4}$,令y=0,得x2-3x+$\frac{5}{4}$=0,解得x=$\frac{1}{2}$或$\frac{5}{2}$,
∴A($\frac{1}{2}$,0),B($\frac{5}{2}$,0),
令x=0,得y=$\frac{5}{4}$,
∴C(0,$\frac{5}{4}$).
設直線BC的解析式為y=kx+b,
則有$\left\{\begin{array}{l}{\frac{5}{2}k+b=0}\\{b=\frac{5}{4}}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-\frac{1}{2}}\\{b=\frac{5}{4}}\end{array}\right.$,
∴直線BC的解析式為y=-$\frac{1}{2}$x+$\frac{5}{4}$.
(2)設D坐標為(m,m2-3m+$\frac{5}{4}$),
∴點E坐標為(m,-$\frac{1}{2}$m+$\frac{5}{4}$),設DE的長為d,
∵D是直線BC下方的一點,
∴d=(-$\frac{1}{2}$m+$\frac{5}{4}$)-(m2-3m+$\frac{5}{4}$)=-m2+$\frac{5}{2}$m=-(m-$\frac{5}{4}$)2+$\frac{25}{16}$,
∴當m=$\frac{5}{4}$時,線段DE的長度最長,此時D($\frac{5}{4}$,-$\frac{15}{16}$).
點評 本題考查拋物線與x軸的交點、一次函數的應用、待定系數法等知識,解題的關鍵是熟練掌握待定系數法確定函數解析式,學會構建二次函數解決最值問題,屬于中考常考題型.


 探究與鞏固河南科學技術出版社系列答案
探究與鞏固河南科學技術出版社系列答案科目:初中數學 來源: 題型:解答題
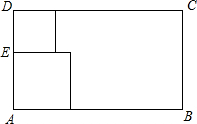 如圖所示,從一張矩形紙較短的邊上找一點E.過點E剪下兩個正方形,它們的邊長分別是AE,DE,要使剪下的兩個正方形的面積和最小,點E應選在何處?
如圖所示,從一張矩形紙較短的邊上找一點E.過點E剪下兩個正方形,它們的邊長分別是AE,DE,要使剪下的兩個正方形的面積和最小,點E應選在何處?查看答案和解析>>
科目:初中數學 來源: 題型:填空題
 如圖,已知P是兩直角邊分別為3cm、4cm的Rt△ABC斜邊AB上的任意一點,以CP為直徑作圓,則該圓的面積y(cm2)與CP的長x(cm)之間的函數關系式是y=$\frac{1}{4}$πx2,自變量x的取值范圍是2.4≤x≤4,y的最小值是1.44π,y的最大值是4π.
如圖,已知P是兩直角邊分別為3cm、4cm的Rt△ABC斜邊AB上的任意一點,以CP為直徑作圓,則該圓的面積y(cm2)與CP的長x(cm)之間的函數關系式是y=$\frac{1}{4}$πx2,自變量x的取值范圍是2.4≤x≤4,y的最小值是1.44π,y的最大值是4π.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 1個 | B. | 2個 | C. | 3個 | D. | 4個 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 若y是x的函數,那么x也是y的函數 | |
| B. | 兩個變量之間的函數關系一定能用數學式子表達 | |
| C. | 若y是x的函數,則當y取一個值時,一定有唯一的x值與它對應 | |
| D. | 一個人的身高也可以看作他年齡的函數 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com