Question

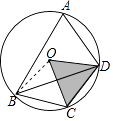
【題目】如圖，四邊形ABCD內接于⊙O，C為 的中點，若∠CBD=30°，⊙O的半徑為12．
（1）求∠BAD的度數；
（2）求扇形OCD的面積．

Answer 1

【答案】
（1）解：∵C是為 的中點，

∴ =2 ，

∴∠BAD=∠COD，

∵ = ，

∴∠COD=2∠CBD，

∴∠BAD=2∠CBD，

∵∠CBD=30°，

∴∠BAD=60°

（2）解：∵ = ，

∴∠COD=2∠CBD，

∵∠CBD=30°，

∴∠COD=60°，

則S扇形OCD= =24π．

【解析】（1）根據題意可得 =2 ，進而可得∠BAD=∠COD，∠BAD=2∠CBD，再由條件∠CBD=30°可得∠BAD的度數；（2）根據圓周角定理可得∠COD=60°，再根據扇形的面積公式可得答案．
【考點精析】掌握圓內接四邊形的性質和扇形面積計算公式是解答本題的根本，需要知道把圓分成n(n≥3):1、依次連結各分點所得的多邊形是這個圓的內接正n邊形2、經過各分點作圓的切線，以相鄰切線的交點為頂點的多邊形是這個圓的外切正n邊形；在圓上，由兩條半徑和一段弧圍成的圖形叫做扇形；扇形面積S=π（R2-r2）．