
【題目】已知:如圖1,拋物線的頂點為M,平行于x軸的直線與該拋物線交于點A,B(點A在點B左側),根據對稱性△AMB恒為等腰三角形,我們規定:當△AMB為直角三角形時,就稱△AMB為該拋物線的“完美三角形”.
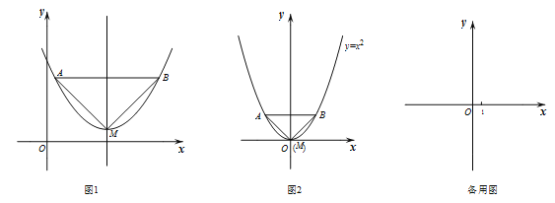
(1)①如圖2,求出拋物線![]() 的“完美三角形”斜邊AB的長;
的“完美三角形”斜邊AB的長;
②拋物線![]() 與
與![]() 的“完美三角形”的斜邊長的數量關系是 ;
的“完美三角形”的斜邊長的數量關系是 ;
(2)若拋物線![]() 的“完美三角形”的斜邊長為4,求a的值;
的“完美三角形”的斜邊長為4,求a的值;
(3)若拋物線![]() 的“完美三角形”斜邊長為n,且
的“完美三角形”斜邊長為n,且![]() 的最大值為-1,求m,n的值.
的最大值為-1,求m,n的值.
【答案】(1)、AB=2;相等;(2)、a=±![]() ;(3)、
;(3)、![]() ,∴
,∴![]() .
.
【解析】
試題分析:(1)、過點B作BN⊥x軸于N,由題意可知△AMB為等腰直角三角形,設出點B的坐標為(n,-n),根據二次函數得出n的值,然后得出AB的值;(2)、根據拋物線的性質相同得出拋物線的完美三角形全等,從而得出點B的坐標,得出a的值;(3)、根據最大值得出mn-4m-1=0,根據拋物線的完美三角形的斜邊長為n得出點B的坐標,然后代入拋物線求出m和n的值.
試題解析:(1)、①過點B作BN⊥x軸于N,由題意可知△AMB為等腰直角三角形,AB∥x軸,
易證MN=BN,設B點坐標為(n,-n),代入拋物線![]() ,得
,得![]() ,
,
∴![]() ,
,![]() (舍去),∴拋物線
(舍去),∴拋物線![]() 的“完美三角形”的斜邊
的“完美三角形”的斜邊![]()
②相等;
(2)、∵拋物線![]() 與拋物線
與拋物線![]() 的形狀相同,
的形狀相同,
∴拋物線![]() 與拋物線
與拋物線![]() 的“完美三角形”全等,
的“完美三角形”全等,
∵拋物線![]() 的“完美三角形”斜邊的長為4,∴拋物線
的“完美三角形”斜邊的長為4,∴拋物線![]() 的“完美三角形”斜邊的長為4,
的“完美三角形”斜邊的長為4,
∴B點坐標為(2,2)或(2,-2),∴![]() .
.
(3)、∵![]() 的最大值為-1,∴
的最大值為-1,∴![]() ,
,
∴![]() ,∵拋物線
,∵拋物線![]() 的“完美三角形”斜邊長為n,
的“完美三角形”斜邊長為n,
∴拋物線![]() 的“完美三角形”斜邊長為n,∴B點坐標為
的“完美三角形”斜邊長為n,∴B點坐標為![]() ,
,
∴代入拋物線![]() ,得
,得![]() ,∴
,∴![]() (不合題意舍去),
(不合題意舍去),
∴![]() ,∴
,∴![]()


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】今年“地球停電一小時”活動的某地區燭光晚餐中,設座位有x排,每排坐30人,則有8人無座位;每排坐31人,則空26個座位.則下列方程正確的是( ) .
A. 30x-8=31x+26 B. 30x+8=31x+26
C. 30x-8=31x-26 D. 30x+8=31x-26
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,![]() 是⊙
是⊙![]() 的直徑,
的直徑,![]() 是⊙
是⊙![]() 上一點,
上一點,![]() 是
是![]() 的中點,過點D作⊙O的切線,與AB,AC的延長線分別交于點E,F,連結AD.
的中點,過點D作⊙O的切線,與AB,AC的延長線分別交于點E,F,連結AD.
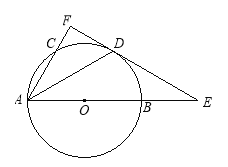
(1)求證:AF⊥EF;
(2)若![]() ,AB=5,求線段BE的長.
,AB=5,求線段BE的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】火星和地球的距離約為34000000千米,用科學記數法表示34000000,應記作( )
A.0.34×108 B.3.4×106 C.3.4×105 D.3.4×107
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com