
【題目】如圖,平面直角坐標系中,若點A(3,0)、B(4,1)到一次函數y=kx+4(k≠0)圖象的距離相等,則k的值為_____.

【答案】k=±1.
【解析】
根據一次函數y=kx+4(k≠0)圖象一定過點(0,4),點A(3,0)、B(4,1)到一次函數y=kx+4(k≠0)圖象的距離相等,可分為兩種情況進行解答,即,①當直線y=kx+4(k≠0)與直線AB平行時,②當直線y=kx+4(k≠0)與直線AB不平行時分別進行解答即可.
一次函數y=kx+4(k≠0)圖象一定過(0,4)點,
①當直線y=kx+4(k≠0)與直線AB平行時,如圖1,
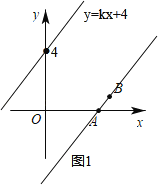
設直線AB的關系式為y=kx+b,
把A(3,0),B(4,1)代入得,
![]() ,解得,k=1,b=﹣3,
,解得,k=1,b=﹣3,
∴一次函數y=kx+4(k≠0)中的k=1;
②當直線y=kx+4(k≠0)與直線AB不平行時,如圖2,
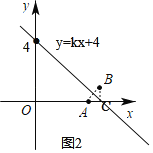
根據題意,直線y=kx+4(k≠0)垂直平分線段![]() ,此時一定經過點C,
,此時一定經過點C,
∴點C的坐標為(4,0),代入得,
4k+4=0,解得,k=﹣1,
因此,k=1或k=﹣1.
故答案為:k=±1.


科目:初中數學 來源: 題型:
【題目】(問題背景)如圖1所示,在![]() 中,
中,![]() ,
,![]() ,點D為直線
,點D為直線![]() 上的個動點(不與B、C重合),連結
上的個動點(不與B、C重合),連結![]() ,將線段
,將線段![]() 繞點D按順時針方向旋轉90°,使點A旋轉到點E,連結
繞點D按順時針方向旋轉90°,使點A旋轉到點E,連結![]() .
.
(問題初探)如果點D在線段![]() 上運動,通過觀察、交流,小明形成了以下的解題思路:過點E作
上運動,通過觀察、交流,小明形成了以下的解題思路:過點E作![]() 交直線
交直線![]() 于F,如圖2所示,通過證明
于F,如圖2所示,通過證明![]() ______,可推證
______,可推證![]() 是_____三角形,從而求得
是_____三角形,從而求得![]() ______°.
______°.
(繼續探究)如果點D在線段![]() 的延長線上運動,如圖3所示,求出
的延長線上運動,如圖3所示,求出![]() 的度數.
的度數.
(拓展延伸)連接![]() ,當點D在直線
,當點D在直線![]() 上運動時,若
上運動時,若![]() ,請直接寫出
,請直接寫出![]() 的最小值.
的最小值.
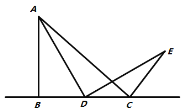
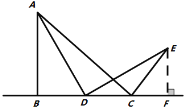
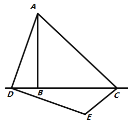
圖1 圖2 圖3
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在東西方向的海岸線l上有一長為1km的碼頭MN(如圖),在碼頭西端M的正西19.5km處有一觀察站A.某時刻測得一艘勻速直線航行的輪船位于A的北偏西30°,且與A相距40km的B處;經過1小時20分鐘,又測得該輪船位于A的北偏東60°,且與A相距![]() km的C處.
km的C處.
(1)求該輪船航行的速度(保留精確結果);
(2)如果該輪船不改變航向繼續航行,那么輪船能否正好行至碼頭MN靠岸?請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】榮昌公司要將本公司100噸貨物運往某地銷售,經與春晨運輸公司協商,計劃租用甲,乙兩種型號的汽車共6輛,用這6輛汽車一次將貨物全部運走,其中每輛甲型汽車最多能裝該種貨物16噸,每輛乙型汽車最多能裝該種貨物18噸.已知租用1輛甲型汽車和2輛乙型汽車共需費用2500元;租用2輛甲型汽車和1輛乙型汽車共需費用2450元,且同一種型號汽車每輛租車費用相同.
(1)求租用一輛甲型汽車,一輛乙型汽車的費用分別是多少元?
(2)若榮昌公司計劃此次租車費用不超過5000元.通過計算求出該公司有幾種租車方案?請你設計出來,并求出最低的租車費用.
(3)該商業公司生產的此時令商品每件成本為15元,經過市場調研發現,這種商品在未來20天內的日銷量m(件)與時間t(天)的函數關系:m=﹣2t+100;該商品每天的價格y(元/件)與時間t(天)的函數關系為:y=![]() t+20(1≤t≤20),其中t取整數;在實際銷售的前20天中,該公司決定每銷售一件商品就捐贈a元利潤(a<4)給希望工程.公司通過銷售記錄發現,前20天中,每天扣除捐贈后的日銷售利潤時間t(天)的增大而增大(含20天的日銷售利潤和第19天的日銷售利潤相等的情況),求a的最小值.
t+20(1≤t≤20),其中t取整數;在實際銷售的前20天中,該公司決定每銷售一件商品就捐贈a元利潤(a<4)給希望工程.公司通過銷售記錄發現,前20天中,每天扣除捐贈后的日銷售利潤時間t(天)的增大而增大(含20天的日銷售利潤和第19天的日銷售利潤相等的情況),求a的最小值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】規定:sin(-x)=-sinx,cos(-x)=cosx,sin(x+y)=sinx·cosy+cosx·siny.據此判斷下列等式成立的是_________(填序號).
①cos(-60°)=—cos60°=![]()
②sin75°=sin(30°+45°)=sin30°·cos45°+cos30°·sin45°=![]()
③sin2x=sin(x+x)=sinx·cosx+cosx·sinx=2sinx·cosx;
④sin(x-y)=sinx·cosy-cosx·siny.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一輛汽車在某次行駛過程中,油箱中的剩余油量y(升)與行駛路程x(千米)之間是一次函數關系,其部分圖象如圖所示.
(1)求y關于x的函數關系式;(不需要寫定義域)
(2)已知當油箱中的剩余油量為8升時,該汽車會開始提示加油,在此次行駛過程中,行駛了500千米時,司機發現離前方最近的加油站有30千米的路程,在開往該加油站的途中,汽車開始提示加油,這時離加油站的路程是多少千米?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】商場某種商品平均每天可銷售30件,每件盈利50元。為了盡快減少庫存,商場決定采取適當的降價措施。經調查發現,每件商品每降價1元,商場平均每天可多售出2件。設每件商品降價![]() 元。據此規律,請回答:
元。據此規律,請回答:
(1)商場日銷售量增加_____件,每件商品盈利_____元(用含![]() 的代數式表示)。
的代數式表示)。
(2)在上述條件不變、銷售正常情況下,每件商品降價多少元時,商場日盈利可達到2100元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某公司生產![]() 、
、![]() 兩種機械設備,每臺
兩種機械設備,每臺![]() 種設備的成本是
種設備的成本是![]() 種設備的1.5倍,公司若投入16萬元生產
種設備的1.5倍,公司若投入16萬元生產![]() 種設備,36萬元生產
種設備,36萬元生產![]() 種設備,則可生產兩種設備共10臺,請解答下列問題:
種設備,則可生產兩種設備共10臺,請解答下列問題:
(1)![]() 、
、![]() 兩種設備每臺的成本分別是多少萬元?
兩種設備每臺的成本分別是多少萬元?
(2)![]() 、
、![]() 兩種設備每臺的售價分別是6萬元、10萬元,且該公司生產兩種設備各30臺,現公司決定對兩種設備優惠出售,
兩種設備每臺的售價分別是6萬元、10萬元,且該公司生產兩種設備各30臺,現公司決定對兩種設備優惠出售,![]() 種設備按原來售價8折出售,B種設備在原來售價的基礎上優惠10%,若設備全部售出,該公司一共獲利多少萬元?
種設備按原來售價8折出售,B種設備在原來售價的基礎上優惠10%,若設備全部售出,該公司一共獲利多少萬元?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com