Question

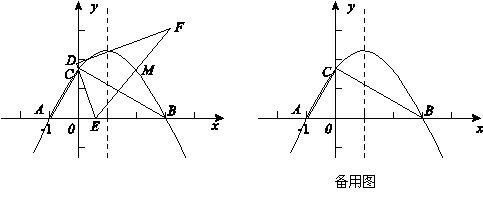
在平面直角坐標系xOy中，一塊含60°角的三角板作如圖擺放，斜邊AB在x軸上，直角頂點C在y軸正半軸上，已知點A（-1，0）．

   （1）請直接寫出點B，C的坐標：B（   ，   ），C（   ，   ）；

（2）求經過A，B，C三點的拋物線解析式；

   （3）現有與上述三角板完全一樣的三角板DEF（其中∠EDF=90°，∠DEF=60°），把頂點E放在線段AB上（點E是不與A，B兩點重合的動點），并使ED所在直線經過點C．此時，EF所在直線與（2）中的拋物線交于第一象限的點M．當AE=2時，拋物線的對稱軸上是否存在點P使△PEM是等腰三角形，若存在，請求出點P的坐標；若不存在，請說明理由．

 

Answer 1

解：（1）B（3，0），C（0，）；

（2）∵點A（-1，0），B（3，0），

　　 ∴可設經過A，B，C三點的拋物線的解析式為，

　　 ∵點C（0，）也在此拋物線上，

　　 ∴， 解得：，

　　 ∴此拋物線的解析式為即．

　 （3）存在．

∵AE=2，

∴OE=1，

∴E（1，0），此時，△CAE為等邊三角形．

∴∠AEC=∠A=60°．

又∵∠CEM=60°，

∴∠MEB=60°．
∴點C與點M關于拋物線的對稱軸對稱．

∵C（0，），

∴M（2，）．

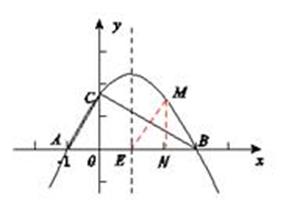
過M作MN⊥x軸于點N（2，0），

∴MN=．

∴ EN=1．

∴．

若△PEM為等腰三角形，則：

ⅰ）當EP=EM時，∵EM=2，且點P在直線x=1上，∴P（1，2）或P（1，-2）．

ⅱ）當EM=PM時，點M在EP的垂直平分線上，∴P（1，）．

ⅲ）當PE=PM時，點P是線段EM的垂直平分線與直線x=1的交點，∴P（1，）．

∴綜上所述，存在P點坐標為（1，2）或（1，-2）或（1，）或（1，）時，△EPM為等腰三角形．

九年級數學參考答案 第4頁（共4頁）