
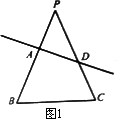
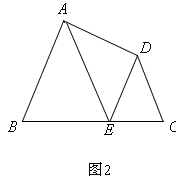
我們把由不平行于底邊的直線截等腰三角形的兩腰所得的四邊形稱為“準等腰梯形”。如圖1,四邊形ABCD即為“準等腰梯形”。其中∠B=∠C。
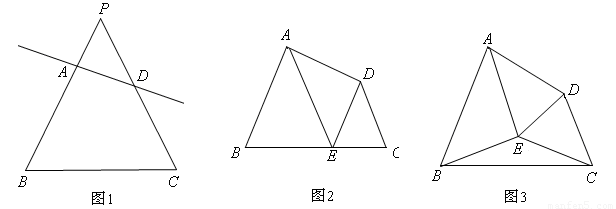
(1)在圖1所示的“準等腰梯形”ABCD中,選擇合適的一個頂點引一條直線將四邊形ABCD分割成一個等腰梯形和一個三角形或分割成一個等腰三角形和一個梯形(畫出一種示意圖即可)。
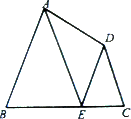
(2)如圖2,在“準等腰梯形”ABCD中,∠B=∠C,E為邊BC上一點,若AB∥DE,AE∥DC,求證: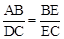
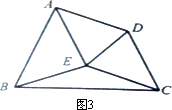
(3)在由不平行于BC的直線截ΔPBC所得的四邊形ABCD中,∠BAD與∠ADC的平分線交于點E,若EB=EC,請問當點E在四邊形ABCD內部時(即圖3所示情形),四邊形ABCD是不是“準等腰梯形”,為什么?若點E不在四邊形ABCD內部時,情況又將如何?寫出你的結論(不必說明理由)
見解析
【解析】解:(1)作圖如下:(畫出一種示意圖即可,答案不唯一)
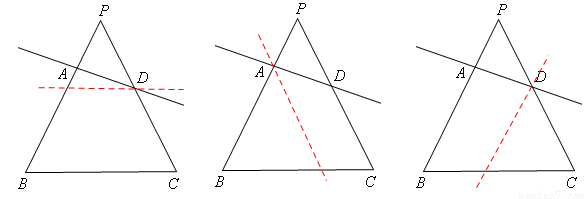
(2)證明:∵AE∥DC,∴∠AEB=∠C。
又∵AB∥DE,∴∠B=∠DEC。∴△ABE∽△DCE。
∴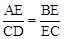 。
。
又∵∠B=∠C,∴∠B=∠AEB。∴AB=AE。
∴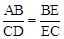 。
。
(3)如圖,過點E分別作EF⊥AB,EG⊥AD,AH⊥CD,垂足分別 是F,G,H,
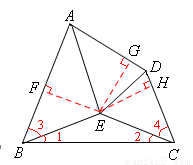
∵AE平分∠BAD,∴EF=EG。
又∵ED平分∠BAD,∴EG=EH。∴EF= EH。
又∵EB=EC,∴Rt△BEF≌Rt△CEF(HL)。∠3=∠4。
又∵EB=EC,∴∠1=∠2。
∴∠1+∠3=∠2+∠4,即∠ABC=∠DCB。
∴四邊形ABCD是 “準等腰梯形”。
當點E不在四邊形ABCD內部時,有兩種情況:
當點E在四邊形ABCD的邊BC上時,四邊形ABCD仍為 “準等腰梯形”;
當點E在四邊形ABCD的外部時,四邊形ABCD仍為 “準等腰梯形”。
(1)根據平行線的性質,過點D作BC的平行線或點D作PB的平行線或點A作PC的平行線,都能線將四邊形ABCD分割成一個等腰梯形和一個三角形或分割成一個等腰三角形和一個梯形,作法不唯一。
(2)易證△ABE∽△DCE,可得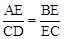 ,由∠B=∠C可證得AB=AE,從而得證。
,由∠B=∠C可證得AB=AE,從而得證。
(3)過點E分別作EF⊥AB,EG⊥AD,AH⊥CD,垂足分別 是F,G,H,根據角平分線上的點到角的兩邊距離相等的性質,可得EF=EG= EH,從而可由HL證得 Rt△BEF≌Rt△CEF,從而∠3=∠4;由EB=EC,得∠1=∠2,根據等量加等量和相等,得∠ABC=∠DCB,即四邊形ABCD是 “準等腰梯形”。
分點E在四邊形ABCD的邊BC上和點E在四邊形ABCD的外部兩種情況研究。


科目:初中數學 來源: 題型:

| AB |
| DC |
| BE |
| EC |
查看答案和解析>>
科目:初中數學 來源:2013年安徽省高級中等學校招生考試數學 題型:044
我們把由不平行于底邊的直線截等腰三角形的兩腰所得的四邊形稱為“準等腰梯形”.如圖1,四邊形ABCD即為“準等腰梯形”.其中∠B=∠C.
(1)在圖1所示的“準等腰梯形”ABCD中,選擇合適的一個頂點引一條直線將四邊形ABCD分割成一個等腰梯形和一個三角形或分割成一個等腰三角形和一個梯形(畫出一種示意圖即可).
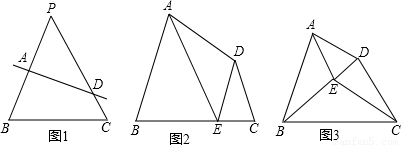
(2)如圖2,在“準等腰梯形”ABCD中,∠B=∠C,E為邊BC上一點,若AB∥DE,AE∥DC,求證:![]()
(3)在由不平行于BC的直線截△PBC所得的四邊形ABCD中,∠BAD與∠ADC的平分線交于點E,若EB=EC,請問當點E在四邊形ABCD內部時(即圖3所示情形),四邊形ABCD是不是“準等腰梯形”,為什么?若點E不在四邊形ABCD內部時,情況又將如何?寫出你的結論(不必說明理由)?
查看答案和解析>>
科目:初中數學 來源:2013年初中畢業升學考試(安徽卷)數學(帶解析) 題型:解答題
我們把由不平行于底邊的直線截等腰三角形的兩腰所得的四邊形稱為“準等腰梯形”。如圖1,四邊形ABCD即為“準等腰梯形”。其中∠B=∠C。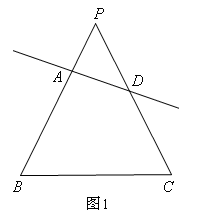
(1)在圖1所示的“準等腰梯形”ABCD中,選擇合適的一個頂點引一條直線將四邊形ABCD分割成一個等腰梯形和一個三角形或分割成一個等腰三角形和一個梯形(畫出一種示意圖即可)。
(2)如圖2,在“準等腰梯形”ABCD中,∠B=∠C,E為邊BC上一點,若AB∥DE,AE∥DC,求證: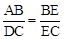
(3)在由不平行于BC的直線截ΔPBC所得的四邊形ABCD中,∠BAD與∠ADC的平分線交于點E,若EB=EC,請問當點E在四邊形ABCD內部時(即圖3所示情形),四邊形ABCD是不是“準等腰梯形”,為什么?若點E不在四邊形ABCD內部時,情況又將如何?寫出你的結論(不必說明理由)
查看答案和解析>>
科目:初中數學 來源:2013年安徽省中考數學試卷(解析版) 題型:解答題
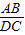 =
=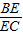 ;
;查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com