
【題目】正方形ABCD和正方形CEFG如圖1所示,其中B、C、E在一條直線上,O是AF的中點,連接OD、OG
(1)探究OD與OG的位置關系![]() 的值;(寫出結論不用證明)
的值;(寫出結論不用證明)
(2)如圖2所示,將正方形ABCD和正方形CEFG改為菱形ABCD和菱形CEFG,且∠ABC=∠DCE=120°,探究OD與OG的位置關系,及![]() 的比值;
的比值;
(3)拓展探索:把圖1中的正方形CEFG繞C順時針旋轉小于90°的角后,其他條件均不變,問第1問中的兩個結論是否發生變化?(寫出結論不用證明)

【答案】(1)OD⊥OG. ![]() =1;(2)OD⊥OG,
=1;(2)OD⊥OG, ![]() ,理由見解析;(3)第(1)問中的兩個結論沒有發生變化.
,理由見解析;(3)第(1)問中的兩個結論沒有發生變化.
【解析】試題分析:
(1)延長GO交AD于點H,由已知條件易證△AHO≌△FGO,從而可得GO=HO,GF=AH=GC,結合AD=CD可得DH=DG,結合∠GDH=90°即可得到OD⊥OG,OD=OG,從而可得![]() ;
;
(2)延長GO交AD于H,同(1)易證△AHO≌△FGO,從而同理可得OD⊥OG,由已知條件可證得∠ODG=60°,則∠DGO=30°,結合∠DOG=90°,即可得到tan∠DGO=![]() ;
;
(3)第(1)問中的兩個結論沒有發生變化,如圖3,過點F作FH∥AD交DO的延長線于點H,延長DC交FH于點M,連接GH,DG,這樣由已知易證△ADO≌△FHO,從而可得FH=AD=CD,DO=HO;再由∠GCE=∠CMN=∠E=∠EFG=90°,可得∠DCG+∠MCN=∠MCN+∠CNM=∠FNE+∠NEF=∠NEF+∠GFH=90°,結合∠CNM=∠FNE可得∠DCG=∠CNM=∠GFH即可證得△DCG≌△HFG,進一步即可證得△DGH是等腰直角三角形,即可由此得到DO=GO,且DO⊥GO,從而說明(1)中結論仍然成立了.
試題解析:
(1)OD⊥OG, ![]() =1,理由如下:
=1,理由如下:
如圖1,延長GO交AD于點H,由已知可得OA=OF,AD∥GF,
∴∠OAH=∠OFG,∠AHO=∠FGO,
∴△AHO≌△FGO,
∴OH=OG,AH=GF=GC,
又∵AD=CD,
∴DH=DG,
∴DO⊥OG,
∵∠ADC=90°,∴DO=OG,
∴![]() ;
;

(2)OD⊥OG , ![]() ,理由如下:
,理由如下:
如圖2所示,延長GO交AD于H.

∵菱形ABCD和菱形CEFG,且B、C、E在一條直線上,
∴AD∥GF,
∵O是AF的中點,
∴△AOH≌△FOG,
∴AH=CF,HO=OG,
∵CF=CG,AD=CD,
∴DH=DG,
∴DO⊥HG且∠ODG=60°,
∴![]() ;
;
(3)第(1)問中的兩個結論沒有發生變化,理由如下:
如圖3,過點F作FH∥AD交DO的延長線于點H,延長DC交FH于點M,連接GH,DG,
∴∠ADO=∠FHO,∠DAO=∠HFO,
又∵AO=FO,
∴△ADO≌△FHO,
∴FH=AD=CD,DO=HO,
∵∠GCE=∠CMN=∠E=∠EFG=90°,
∴∠DCG+∠MCN=∠MCN+∠CNM=∠FNE+∠NEF=∠NEF+∠GFH=90°,
又∵∠CNM=∠FNE,
∴∠DCG=∠CNM=∠GFH,
又∵DC=FH,CG=FG,
∴△DCG≌△HFG,
∴DG=HG/span>,∠DGC=∠HGF,
∵∠CGH+∠HFG=∠CGF=90°,
∴∠CGH+∠DGC=∠=90°,
∴△DGH是等腰直角三角形,
又∵DO=HO,
∴DO=GO,且DO⊥GO,
∴![]() ,
,
∴(1)中結論仍然成立.



科目:初中數學 來源: 題型:
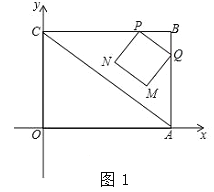
【題目】已知矩形OABC在如圖所示平面直角坐標系中,點B的坐標為(4,3),連接AC.動點P從點B出發,以2cm/s的速度,沿直線BC方向運動,運動到C為止(不包括端點B、C),過點P作PQ∥AC交線段BA于點Q,以PQ為邊向下作正方形PQMN,設正方形PQMN與△ABC重疊部分圖形面積為S(cm2),設點P的運動時間為t(s).
(1)請用含t的代數式表示BQ長和N點的坐標;
(2)求S與t之間的函數關系式,并指出t的取值范圍;
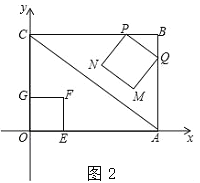
(3)如圖2,點G在邊OC上,且OG=1cm,在點P從點B出發的同時,另有一動點E從點O出發,以2cm/s的速度,沿x軸正方向運動,以OG、OE為一組鄰邊作矩形OEFG.試求當點F落在正方形PQMN的內部(不含邊界)時t的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,平面上有點A、點O和直線PQ,其中網格正方形的邊長為1個單位,在網格中完成下列畫圖.(不必寫出畫法,保留畫圖痕跡,并寫出結論)

(1)將點A向右平移3個單位可到達點B,再向上平移2個單位可到達點C,標出點B、點C,并聯結AB、BC和AC,畫出三角形ABC;
(2)畫出三角形ABC關于直線PQ的軸對稱的圖形;
(3)畫出三角形ABC關于點O的中心對稱的圖形.
結論:
(1) ;
(2)三角形 是三角形ABC關于直線PQ的軸對稱的圖形;
(3)三角形 是三角形ABC關于點O的中心對稱的圖形.
查看答案和解析>>
科目:初中數學 來源: 題型:
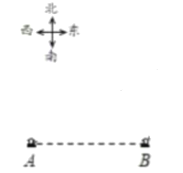
【題目】如圖,A地和B地都是海上觀測站,B地在A地正東方向,且A、B兩地相距2海里. 從A地發現它的北偏東60°方向有一艘船C,同時,從B地發現船C在它的北偏東30°方向.
(1)在圖中畫出船C所在的位置;(要求用直尺與量角器作圖,保留作圖痕跡)
(2)已知三角形的內角和等于180°,求∠ACB的度數.
(3)此時船C與B地相距______海里.(只需寫出結果,不需說明理由)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】重慶某中學組織七、八、九年級學生參加“直轄20年,點贊新重慶”作文比賽,該校將收到的參賽作文進行分年級統計,繪制了如圖1和如圖2兩幅不完整的統計圖,根據圖中提供的信息完成以下問題.
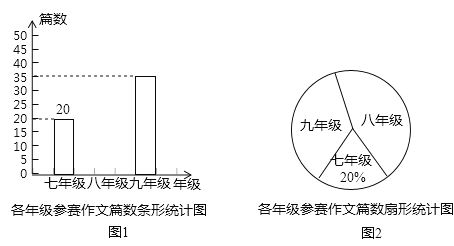
(1)扇形統計圖中九年級參賽作文篇數對應的圓心角是 度,并補全條形統計圖;
(2)經過評審,全校有4篇作文榮獲特等獎,其中有一篇來自七年級,學校準備從特等獎作文中任選兩篇刊登在校刊上,請利用畫樹狀圖或列表的方法求出七年級特等獎作文被選登在校刊上的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,四邊形OABC 的邊OC 、OA 分別與 x 軸、 y 軸重合, AOC 90,BCO 45, AB // OC , BC 6 ![]() ,點C 的坐標為 9,0.
,點C 的坐標為 9,0.
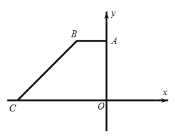

(1)求點 B 的坐標;
(2)若直線 DE 交四邊形的對角線 BO 于點 D ,交 y 軸于點 E ,且OE 2 , OD 2BD ,求:
① ODE 的面積;
②點 D 的坐標.
(3)在(2)的條件下,坐標平面內是否存在點 P ,使以O 、E 、P 、D 為頂點的四邊形是平行四邊形? 若存在,請直接寫出點 P 的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,在∠A內部有一點P,連接BP、CP,請回答下列問題:

(1)求證:∠P=∠1+∠A+∠2;
(2)如圖2,利用上面的結論,在五角星中,∠A+∠B+∠C+∠D+∠E= ;
(3)如圖3,如果在∠BAC間有兩個向上突起的角,請你根據前面的結論猜想∠1、∠2、∠3、∠4、∠5、∠A之間有什么等量關系,直接寫出結論即可.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,矩形OABC的頂點A,C分別在x軸,y軸的正半軸上,且OA=4,OC=3,若拋物線經過O,A兩點,且頂點在BC邊上,對稱軸交AC于點D,動點P在拋物線對稱軸上,動點Q在拋物線上.
(1)求拋物線的解析式;
(2)當PO+PC的值最小時,求點P的坐標;
(3)是否存在以A,C,P,Q為頂點的四邊形是平行四邊形?若存在,請直接寫出P,Q的坐標;若不存在,請說明理由.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com