
【題目】現計劃把甲種貨物1240噸和乙種貨物880噸用一列貨車運往某地,已知這列貨車掛在A、B兩種不同規格的貨車廂共40節,使用A型車廂每節費用為6000元,使用B型車廂每節費用為8000元.
(1)設運送這批貨物的總費用為y萬元,這列貨車掛A型車廂x 節,試定出用車廂節數x表示總費用y的公式.
(2)如果每節A型車廂最多可裝甲種貨物35噸和乙種貨物15噸,每節B型車廂最多可裝甲種貨物25噸和乙種貨物35噸,裝貨時按此要求安排A、B兩種車廂的節數,那么共有哪幾種安排車廂的方案?
【答案】(1) y=32-0.2x;(2) 共有三種方案,A、B兩種車廂的節數分別為24節、16節或25節、15節或26節、14節
【解析】試題分析:(1)總費用=0.6×A型車廂節數+0.8×B型車廂節數.
(2)應分別表示出兩類車廂能裝載的甲乙兩種貨物的質量.35×A型車廂節數+25×B型車廂節數≥1240;15×A型車廂節數+35×B型車廂節數≥880.
試題解析:(1)6000元=0.6萬元,8000元=0.8萬元,
設用A型車廂x節,則用B型車廂(40x)節,總運費為y萬元,
依題意,得y=0.6x+0.8(40x)=0.2x+32;
(2)依題意,得 ,
,
解得: ![]() ,
,
∴24x26,
∵x取整數,故A型車廂可用24節或25節或26節,相應有三種裝車方案:
①24節A型車廂和16節B型車廂;
②25節A型車廂和15節B型車廂;
③26節A型車廂和14節B型車廂.


科目:初中數學 來源: 題型:
【題目】如圖1,⊙O的直徑AB=12,P是弦BC上一動點(與點B,C不重合),∠ABC=30°,過點P作PD⊥OP交⊙O于點D.
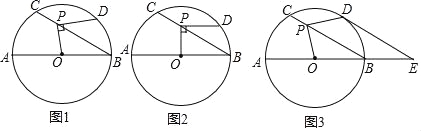
(1)如圖2,當PD∥AB時,求PD的長;
(2)如圖3,當![]() 時,延長AB至點E,使BE=
時,延長AB至點E,使BE=![]() AB,連接DE.
AB,連接DE.
①求證:DE是⊙O的切線;
②求PC的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我市一山區學校為部分家遠的學生安排住宿,將部分教室改造成若干間住房. 如果每間住5人,那么有12人安排不下;如果每間住8人,那么有一間房還余一些床位,問該校可能有幾間住房可以安排學生住宿?住宿的學生可能有多少人?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知點P(x,y)到x軸的距離為2,到y軸的距離為3,且x+y>0,xy<0,則點P的坐標為( )
A.(﹣2,3)B.(2,3)C.(3,﹣2)D.(3,2)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,點E在AC的延長線上,下列條件中能判斷AB∥CD的是( )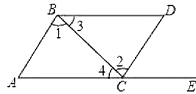
A.∠3=∠A
B.∠l=∠2
C.∠D=∠DCE
D.∠D+∠ACD=180
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com