
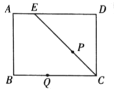
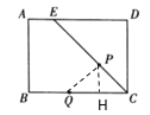
【題目】如圖,在矩形![]() 中,
中,![]() 為
為![]() 上一點,且
上一點,且![]() ,
,![]() ,點
,點![]() ,
,![]() 同時從
同時從![]() 點出發,點
點出發,點![]() 以每秒
以每秒![]() 的速度沿
的速度沿![]() 向終點
向終點![]() 運動,點
運動,點![]() 以每秒2的速度沿折線
以每秒2的速度沿折線![]() 向終點
向終點![]() 運動,設
運動,設![]() 運動的時間為
運動的時間為![]() ,
,![]() ,
,![]() 經過的路線與
經過的路線與![]() 圍成的圖形面積為
圍成的圖形面積為![]() ,則
,則![]() 關于
關于![]() 的圖象大致是( )
的圖象大致是( )
A.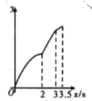 B.
B.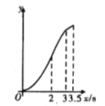 C.
C. D.
D.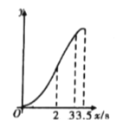
【答案】B
【解析】
根據矩形的性質動點BC=AD=4,AB=CD=3,∠BCD=∠D=90°,AD∥BC,求出∠BCE=∠DEC=45°,由勾股定理求出CE=![]() ,分三段:當
,分三段:當![]() 時,當
時,當![]() 時,當
時,當![]() 時,分別求出函數解析式即可進行判斷.
時,分別求出函數解析式即可進行判斷.
∵四邊形ABCD是矩形,
∴BC=AD=4,AB=CD=3,∠BCD=∠D=90°,AD∥BC,
∵![]() ,
,
∴∠BCE=∠DEC=45°,
∴CE=![]() ,
,
當![]() 時,CP=
時,CP=![]() ,CQ=2x,∴PH=CH=x,
,CQ=2x,∴PH=CH=x,
∴![]() ;
;
當![]() 時,CP=
時,CP=![]() ,BQ=2x-4,
,BQ=2x-4,
過點P作PH⊥BC于H,作MN∥AD,則四邊形ADNM是矩形,四邊形PHCN是矩形,
∴MN=AD=4,PN=CH=x,
∴MP=4-x,
∴![]()
![]()
![]()
=![]() ;
;
當![]() 時,點P與點E重合,
時,點P與點E重合,
∴![]()
![]()
![]() =x+6;
=x+6;
故選:B.



 互動英語系列答案
互動英語系列答案 名牌學校分層周周測系列答案
名牌學校分層周周測系列答案科目:初中數學 來源: 題型:
【題目】如圖,直線![]() 經過點A(3,0)和點B(0,2).
經過點A(3,0)和點B(0,2).
(1)求直線![]() 的解析式;
的解析式;
(2)直線![]() 與函數
與函數![]() 的圖象交于點C(C在第二象限),若ΔCOB的面積與ΔAOB的面積相等,求出m的值.
的圖象交于點C(C在第二象限),若ΔCOB的面積與ΔAOB的面積相等,求出m的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在歌唱比賽中,一位歌手分別轉動如下的兩個轉盤(每個轉盤都被分成3等份)一次,根據指針指向的歌曲名演唱兩首曲目.
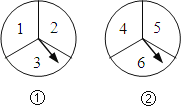
(1)轉動轉盤①時,該轉盤指針指向歌曲“3”的概率是 ;
(2)若允許該歌手替換他最不擅長的歌曲“3”,即指針指向歌曲“3”時,該歌手就選擇自己最擅長的歌曲“1”, 請用樹形圖或列表法中的一種,求他演唱歌曲“1”和“4”的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:在矩形![]() 中,
中,![]() 是對角線,
是對角線,![]() 于點
于點![]() ,
,![]() 于點
于點![]() .
.

(1)如圖1,求證:![]() ;
;
(2)如圖2,當![]() 時,連接
時,連接![]() 、
、![]() ,在不添加任何輔助線的情況下,請直接寫出圖2中四個三角形,使寫出的每個三角形的面積都等于矩形
,在不添加任何輔助線的情況下,請直接寫出圖2中四個三角形,使寫出的每個三角形的面積都等于矩形![]() 面積的
面積的![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,二次函數![]() 的頂點
的頂點![]() 的坐標為
的坐標為![]() .
.
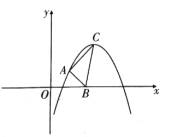
(1)求![]() ,
,![]() 的值;
的值;
(2)已知![]() 點為拋物線上異于
點為拋物線上異于![]() 的一點,且
的一點,且![]() 點橫、縱坐標相等,
點橫、縱坐標相等,![]() 為
為![]() 軸上任意一點,當
軸上任意一點,當![]() 取最小值時,求出
取最小值時,求出![]() 點坐標和此時
點坐標和此時![]() 的面積.
的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】![]() 內接于
內接于![]() ,
,![]() ,連接
,連接![]() ;
;
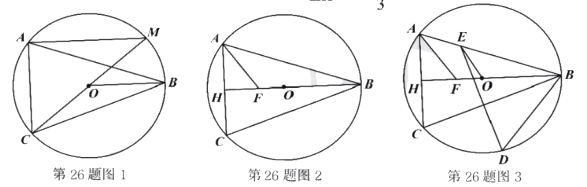
(1)如圖1,連接![]() 并延長交
并延長交![]() 于點
于點![]() ,連接
,連接![]() ,求證:
,求證:![]() ;
;
(2)如圖2,延長![]() 交
交![]() 于點H,點F為BH上一點,連接AF,若
于點H,點F為BH上一點,連接AF,若![]() ,求證:
,求證:![]() ;
;
(3)在(2)的條件下,如圖3,點E為AB上一點,點D為![]() 上一點,連接
上一點,連接![]() 、
、![]() ,若
,若![]() ,若
,若![]() ,
,![]() ,
,![]() ,連接
,連接![]() ,求線段
,求線段![]() 的長.
的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線![]() 的對稱軸是
的對稱軸是![]() .且過點(
.且過點(![]() ,0),有下列結論:①abc>0;②a﹣2b+4c=0;③25a﹣10b+4c=0;④2c-3b>0;⑤a﹣b≥m(am﹣b)(m≠-1);其中所有正確的結論是( )
,0),有下列結論:①abc>0;②a﹣2b+4c=0;③25a﹣10b+4c=0;④2c-3b>0;⑤a﹣b≥m(am﹣b)(m≠-1);其中所有正確的結論是( )
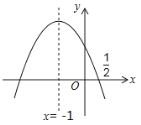
A.①②③B.①③④C.①③④⑤D.②④⑤
查看答案和解析>>
科目:初中數學 來源: 題型:
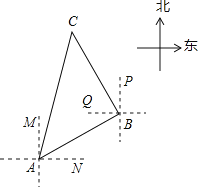
【題目】如圖,一艘船由A港沿北偏東60°方向航行20km至B港,然后再沿北偏西30°方向航行20km至C港.
(1)求A,C兩港之間的距離;(結果保留到0.1km)
(2)確定C港在A港的什么方向(參考數據:![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com