
【題目】如圖,一次函數![]() 的圖像與
的圖像與![]() 軸、
軸、![]() 軸交于
軸交于![]() 、
、![]() 兩點,
兩點,![]() 是
是![]() 軸正半軸上的一個動點,連接
軸正半軸上的一個動點,連接![]() ,將
,將![]() 沿
沿![]() 翻折,點
翻折,點![]() 恰好落在
恰好落在![]() 上,則點
上,則點![]() 的坐標為______.
的坐標為______.
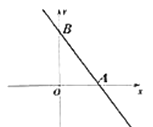
【答案】(![]() ,0)或(24,0)
,0)或(24,0)
【解析】
分兩種情況討論:當點P在OA上時,由O與C關于PB對稱,可得OP=CP,BC=OB=8;當點P在AO延長線上時,由O與C關于PB對稱,可得OP=CP,BC=OB=8,分別依據勾股定理得到方程,解方程即可得到點P的坐標.
解:設點O關于直線PB的對稱點是C.
∵一次函數![]() 的圖象與x軸、y軸交于A、B兩點,
的圖象與x軸、y軸交于A、B兩點,
∴AO=6,BO=8,AB=10.
分兩種情況:
①當點P在OA上時,
由折疊的性質,可得OP=CP,BC=OB=8,∠BCP=∠BOP=90°.
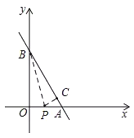
設OP=CP=x,則AP=6x,AC=108=2,
在Rt△ACP中,由勾股定理可得:x2+22=(6x)2,
解得x=![]() ,
,
∴P(![]() ,0);
,0);
②當點P在AO延長線上時,
由折疊的性質,可得OP=CP,BC=OB=8,∠C=∠BOP=90°.
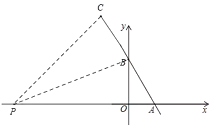
設OP=CP=x,則AP=6+x,AC=10+8=18,
在Rt△ACP中,由勾股定理可得:x2+182=(6+x)2,
解得x=24,
∴P(24,0).
故答案為:(![]() ,0)或(24,0).
,0)或(24,0).


 一諾書業暑假作業快樂假期云南美術出版社系列答案
一諾書業暑假作業快樂假期云南美術出版社系列答案科目:初中數學 來源: 題型:
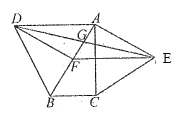
【題目】如圖,分別以![]() 的斜邊
的斜邊![]() ,直角邊
,直角邊![]() 為邊向外作等邊
為邊向外作等邊![]() 和
和![]() ,
,![]() 為
為![]() 的中點,
的中點,![]() ,
,![]() 相交于點
相交于點![]() .若∠BAC=30°,下列結論:①
.若∠BAC=30°,下列結論:①![]() ;②四邊形
;②四邊形![]() 為平行四邊形;③
為平行四邊形;③![]() ;④
;④![]() .其中正確結論的序號是______.
.其中正確結論的序號是______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】隨著科技的進步和網絡資源的豐富,在線學習已成為更多人的自主學習選擇.某校計劃為學生提供以下四類在線學習方式:在線閱讀、在線聽課、在線答題和在線討論.為了解學生需求,該校隨機對本校部分學生進行了“你對哪類在線學習方式最感興趣”的調查,并根據調查結果繪制成如下兩幅不完整的統計圖.
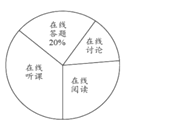
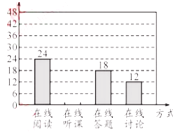
根據圖中信息,解答下列問題:
(1)求本次調查的學生總人數,并補全條形統計圖;
(2)求扇形統計圖中“在線討論”對應的扇形圓心角的度數;
(3)該校共有學生![]() 人,請你估計該校對在線閱讀最感興趣的學生人數.
人,請你估計該校對在線閱讀最感興趣的學生人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小玲和弟弟小東分別從家和圖書館同時出發,沿同一條路相向而行,小玲開始跑步,中途改為步行,到達圖書館恰好用時![]() .小東騎自行車以
.小東騎自行車以![]() 的速度直接回家,兩人離家的路程
的速度直接回家,兩人離家的路程![]() 與各自離開出發地的時間
與各自離開出發地的時間![]() 之間的函數圖象如圖所示,下列說法正確的有幾個.( )
之間的函數圖象如圖所示,下列說法正確的有幾個.( )
①家與圖書館之間的路程為![]() ;
;
②小玲步行的速度為![]() ;
;
③兩人出發以后8分鐘相遇;
④兩人出發以后![]() ,
,![]() 、
、![]() 時相距
時相距![]() .
.
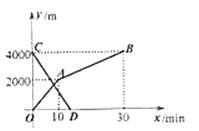
A.1B.2
C.3D.4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知,直線AB∥DC,點P為平面上一點,連接AP與CP.



(1)如圖1,點P在直線AB、CD之間,當∠BAP=60°,∠DCP=20°時,求∠APC.
(2)如圖2,點P在直線AB、CD之間,∠BAP與∠DCP的角平分線相交于點K,寫出∠AKC與∠APC之間的數量關系,并說明理由.
(3)如圖3,點P落在CD外,∠BAP與∠DCP的角平分線相交于點K,∠AKC與∠APC有何數量關系?并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
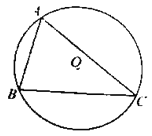
【題目】如圖,⊙O為銳角△ABC的外接圓,半徑為5.
(1)用尺規作圖作出∠BAC的平分線,并標出它與劣弧BC的交點E(保留作圖痕跡,不寫作法);
(2)若(1)中的點E到弦BC的距離為3,求弦CE的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠C=90°,O,D分別為AB,BC上的點,經過A,D兩點的⊙O分別交AB,AC于點E,F,且D為弧EF的中點.
(1)求證:BC與⊙O相切;
(2)當⊙O的半徑r=2,∠CAD=30°時,求劣弧AD的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
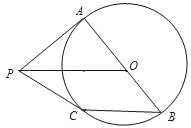
【題目】如圖,AB是⊙O的直徑,PA是⊙O的切線,點C在⊙O上,CB∥PO.
(1)判斷PC與⊙O的位置關系,并說明理由;
(2)若AB=6,CB=4,求PC的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com