
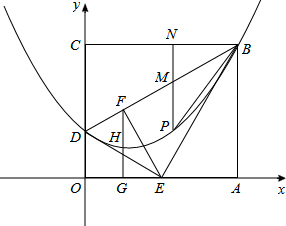
 (2013•德陽)如圖,在平面直角坐標系中有一矩形ABCO(O為原點),點A、C分別在x軸、y軸上,且C點坐標為(0,6),將△BCD沿BD折疊(D點在OC上),使C點落在OA邊的E點上,并將△BAE沿BE折疊,恰好使點A落在BD邊的F點上.
(2013•德陽)如圖,在平面直角坐標系中有一矩形ABCO(O為原點),點A、C分別在x軸、y軸上,且C點坐標為(0,6),將△BCD沿BD折疊(D點在OC上),使C點落在OA邊的E點上,并將△BAE沿BE折疊,恰好使點A落在BD邊的F點上.| 3 |
| 3 |
|
|

| ||
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 2 |
|
|
| 1 |
| 6 |
| ||
| 3 |
| 1 |
| 6 |
| ||
| 3 |
| ||
| 3 |
| 1 |
| 6 |
2
| ||
| 3 |
| ||
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 1 |
| 6 |
| ||
| 3 |
| 3 |
| 1 |
| 6 |
| ||
| 3 |
| 3 |
| 3 |


 一線名師提優(yōu)試卷系列答案
一線名師提優(yōu)試卷系列答案 陽光試卷單元測試卷系列答案
陽光試卷單元測試卷系列答案科目:初中數(shù)學 來源: 題型:
 (2013•德陽)如圖,熱氣球的探測器顯示,從熱氣球A看一棟高樓頂部B的仰角為30°,看這棟高樓底部C的俯角為60°,熱氣球A與高樓的水平距離為120m,這棟高樓BC的高度為( )
(2013•德陽)如圖,熱氣球的探測器顯示,從熱氣球A看一棟高樓頂部B的仰角為30°,看這棟高樓底部C的俯角為60°,熱氣球A與高樓的水平距離為120m,這棟高樓BC的高度為( )查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
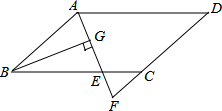 (2013•德陽)如圖,在?ABCD中,AB=6,AD=9,∠BAD的平分線交BC于點E,交DC的延長線于點F,BG⊥AE,垂足為G,若BG=4
(2013•德陽)如圖,在?ABCD中,AB=6,AD=9,∠BAD的平分線交BC于點E,交DC的延長線于點F,BG⊥AE,垂足為G,若BG=4| 2 |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
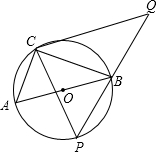 (2013•德陽)如圖,在⊙O上有定點C和動點P,位于直徑AB的異側(cè),過點C作CP的垂線,與PB的延長線交于點Q,已知:⊙O半徑為
(2013•德陽)如圖,在⊙O上有定點C和動點P,位于直徑AB的異側(cè),過點C作CP的垂線,與PB的延長線交于點Q,已知:⊙O半徑為| 5 |
| 2 |
| 3 |
| 4 |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
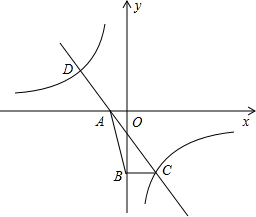 (2013•德陽)如圖,直線y=kx+k(k≠0)與雙曲線y=
(2013•德陽)如圖,直線y=kx+k(k≠0)與雙曲線y=| n+1 |
| x |
| 17 |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com