Question

等邊三角形ABC的邊長為6，在AC，BC邊上各取一點E,F，  連結AF，BE相交于點P.

（1）若AE=CF.

①求證:AF=BE,并求∠APB的度數.

②若AE=2,試求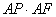的值.

（2）若AF=BE,當點E從點A運動到點C時，試求點P經過的路徑長.

Answer 1

（1）①如圖，∵△ABC是等邊三角形，

  ∴∠C=∠BAC=60°, AB=AC，

又∵AE=CF，

∴△AFC≌△BEA (SAS)，

∴AE=CF,                         

∠1=∠3，

∵∠4=∠2+∠3，

∴∠4=∠2+∠1=∠BAC=60°,

即∠APB=180°-∠4=120°.               

② ∵  ∠C=∠4=60°，∠PAE=∠CAF,

   ∴  △APE∽△ACF,

   ∴，即，所以.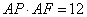  

（2）若AF=BE,有AE=BF或AE=CF兩種情況.

當AE=BF時，如圖2，此時點P經過的路徑是AB邊上的高線CH.

    在Rt△AHC中，, 

∴此時點P經過的路徑長為.

當AE=CF時，如圖3，點P經過的路徑是以A，B為端點的        圓弧，且∠APB=120°,則圓心角∠AOB=120°，

 過點O作OG⊥AB, 在Rt△AOG中，∠AOG=60°，

，

∴.

∴此時點P經過的路徑長為.

所以，點P經過的路徑長為或.