
下表給出了代數式x2+bx+c與x的一些對應值:
| x | …… | -1 | 0 | 1 | 2 | 3 | 4 | …… |
| x2+bx+c | …… | 3 | -1 | 3 | …… |
(1)根據表格中的數據,確定b、c的值,并填齊表格空白處的對應值;
(2)設y=x2 + bx + c的圖象與x軸的交點為A、B兩點(A點在B點左側),與y軸交于點C,P為線段AB上一動點,過P點作PE∥AC交BC于E,連結PC,當△PEC的面積最大時,求P點的坐標.
解:(1)當x=0和x=4時,均有函數值y=3,
∴ 函數的對稱軸為x=2
∴頂點坐標為(2,-1)
即對應關系滿足y=(x-2)2-1,
∴ y=x2-4x+3
∴當x=-1時,y=8;x=1時,y=0;x=3時,y=0
| x | …… | -1 | 0 | 1 | 2 | 3 | 4 | …… |
| x2+bx+c | …… | 8 | 3 | 0 | -1 | 0 | 3 | …… |
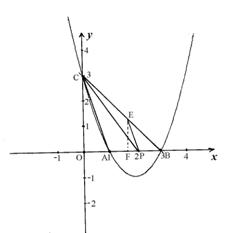 (2) 解:函數圖像與x軸交于A(1,0)、B(3,0);
(2) 解:函數圖像與x軸交于A(1,0)、B(3,0);
與y軸交于點C(0,3)
設P點坐標為(x,0),則PB=3-x
∴S△BCP=![]() (3-x)
(3-x)
∵PE∥AC
∴△BEP∽△BCA 作EF⊥OB于F
∴![]() =
=![]()
即![]() =
=![]()
∴ EF=![]() (3-x)
(3-x)
∴S△BPE=![]() BP?EF=
BP?EF=![]() (3-x)2
(3-x)2
∵S△PEC= S△BCP-S△BPE
∴S△PEC =![]() (3-x)-
(3-x)-![]() (3-x)2
(3-x)2
S△PEC =-![]() x2+3x-
x2+3x-![]() =-
=-![]() (x-2)2+
(x-2)2+![]()
∴當x=2時,y最大=![]()
∴ P點坐標是(2,0)


科目:初中數學 來源: 題型:
| x | … | 0 | 1 | 2 | 3 | 4 | … |
| x2+bx+c | … | 3 | -1 | 3 | … |
查看答案和解析>>
科目:初中數學 來源: 題型:
| x | … | -1 | 0 | 1 | 2 | 3 | 4 | … |
| x2+bx+c | … | 3 | -1 | 3 | … |
查看答案和解析>>
科目:初中數學 來源: 題型:
| x | … | 0 | 1 | 2 | 3 | 4 | … |
| x2+bx+c | … | 3 | -1 | 3 | … |
查看答案和解析>>
科目:初中數學 來源: 題型:
| x | … | -1 | 0 | 1 | 2 | 3 | 4 | … |
| X2+bx+c | … | 3 | -1 | 3 | … |
查看答案和解析>>
科目:初中數學 來源: 題型:
| x | … | 0 | 1 | 2 | 3 | 4 | … |
| x2+bx+c | … | 3 | -1 | 3 | … |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com