
 OA=
OA= ,AB=3,∠OAB=45°,E、F分別是線段OA、AB上的兩動點,且始終保持∠DEF=45°.
,AB=3,∠OAB=45°,E、F分別是線段OA、AB上的兩動點,且始終保持∠DEF=45°.
 ,在Rt△ABM中,已知了∠OAB的度數及AB的長,即可求出AM、BM的長,進而可得到BC、CD的長,由此可求得D點的坐標;
,在Rt△ABM中,已知了∠OAB的度數及AB的長,即可求出AM、BM的長,進而可得到BC、CD的長,由此可求得D點的坐標; 解:(1)過B作BM⊥x軸于M;
解:(1)過B作BM⊥x軸于M; ;
; -
- =
= ,CD=BC-BD=
,CD=BC-BD= ;
;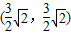 ;(2分)
;(2分)
 ,即:
,即:
 (6分)
(6分)




 ;
;


 (10分)
(10分)



 或1或
或1或 .(12分)
.(12分)

 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源:2010年全國中考數學試題匯編《圖形的相似》(04)(解析版) 題型:解答題
 OA=
OA=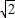 ,AB=3,∠OAB=45°,E、F分別是線段OA、AB上的兩動點,且始終保持∠DEF=45°.
,AB=3,∠OAB=45°,E、F分別是線段OA、AB上的兩動點,且始終保持∠DEF=45°.
查看答案和解析>>
科目:初中數學 來源:2010年全國中考數學試題匯編《三角形》(13)(解析版) 題型:解答題
 OA=
OA= ,AB=3,∠OAB=45°,E、F分別是線段OA、AB上的兩動點,且始終保持∠DEF=45°.
,AB=3,∠OAB=45°,E、F分別是線段OA、AB上的兩動點,且始終保持∠DEF=45°.
查看答案和解析>>
科目:初中數學 來源:2010年湖北省荊州市中考數學試卷(解析版) 題型:解答題
 OA=
OA= ,AB=3,∠OAB=45°,E、F分別是線段OA、AB上的兩動點,且始終保持∠DEF=45°.
,AB=3,∠OAB=45°,E、F分別是線段OA、AB上的兩動點,且始終保持∠DEF=45°.
查看答案和解析>>
科目:初中數學 來源:2010年湖北省荊州市中考數學試卷(解析版) 題型:填空題

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com