
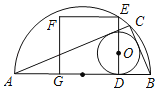
【題目】如圖,AB為半圓的直徑,C是半圓弧上一點,正方形DEFG的一邊DG在直徑AB上,另一邊DE過△ABC的內切圓圓心O,且點E在半圓上.
(1)當正方形的頂點F也在半圓弧上時,半圓的半徑與正方形邊長的比為 ;
(2)當正方形DEFG的面積為100,且△ABC的內切圓⊙O的半徑r=4,求半圓的直徑AB的值;
(3)若半圓的半徑為R,直接寫出⊙O半徑r可取得的最大值.
【答案】(1)![]() ;(2)AB=21;(3)
;(2)AB=21;(3)![]()
【解析】
(1)根據圓和正方形的對稱性可知:![]() ,在直角三角形FGH中,利用勾股定理可得
,在直角三角形FGH中,利用勾股定理可得![]() ,從而用含a的代數式表示半圓的半徑為
,從而用含a的代數式表示半圓的半徑為![]() ,正方形邊長為2a,所以可求得半圓的半徑與正方形邊長的比;
,正方形邊長為2a,所以可求得半圓的半徑與正方形邊長的比;
(2)切點分別為I,J,連接EB、AE,OJ、OI,可得OJCI是正方形,且邊長是4,可設BD=x,AD=y,則BD=BJ=x,AD=AI=y,分別利用直角三角形ABC和直角三角形AEB中的勾股定理和相似比作為相等關系列方程組求解即可求得半圓的直徑AB=21.
(3)根據(2)中得出方程解答即可.
解:(1)如圖,根據圓和正方形的對稱性可知:![]() ,
,
H為半圓的圓心,
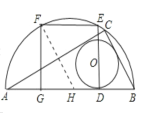
不妨設GH=a,則GF=2a,
在直角三角形FGH中,由勾股定理可得![]() ,由此可得,半圓的半徑為
,由此可得,半圓的半徑為![]() ,正方形邊長為2a,
,正方形邊長為2a,
所以半圓的半徑與正方形邊長的比是![]() ;
;
(2)因為正方形DEFG的面積為100,所以正方形DEFG邊長為10.
切點分別為I,J,連接EB、AE,OI、OJ,
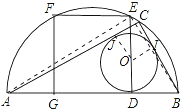
∵AC、BC是⊙O的切線,
∴CJ=CI,∠OJC=∠OIC=90°,
∵∠ACB=90°,
∴四邊形OICJ是正方形,且邊長是4,
設BD=x,AD=y,則BD=BI=x,AD=AJ=y,
在直角三角形ABC中,由勾股定理得(x+4)2+(y+4)2=(x+y)2①;
在直角三角形AEB中,
∵∠AEB=90°,ED⊥AB,
∴△ADE∽△BDE∽△ABE,
∴![]() 即ED2=ADBD,即102=xy②.
即ED2=ADBD,即102=xy②.
解①式和②式,得x+y=21,
即半圓的直徑AB=21;
(3)由(2)可得:![]() ,
,
當點C與點E重合且為半圓弧的中點時,⊙O半徑r可取得的最大值為![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,直線y=x+2經過點A(m,-2),將點A向右平移7個單位長度,得到點B,拋物線![]() 的頂點為C.
的頂點為C.
(1)求m的值和點B的坐標;
(2)求點C的坐標(用含n的代數式表示);
(3)若拋物線與線段AB只有一個公共點,結合函數圖象,求n的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某年五月,我國南方某省A、B兩市遭受嚴重洪澇災害,鄰近縣市C、D決定調運物資支援A、B兩市災區.已知C市有救災物資240噸,D市有救災物資260噸,現將這些救災物資全部調往A、B兩市,A市需要的物資比B市需要的物資少100噸.已知從C市運往A、B兩市的費用分別為每噸20元和25元,從D市運往往A、B兩市的費用分別為每噸15元和30元,設從D市運往B市的救災物資為x噸.
(1)A、B兩市各需救災物資多少噸?
(2)設C、D兩市的總運費為w元,求w與x之間的函數關系式,并寫出自變量x的取值范圍;
(3)經過搶修,從D市到B市的路況得到了改善,縮短了運輸時間,運費每噸減少m元(m>0),其余路線運費不變.若C、D兩市的總運費的最小值不小于10320元,求m的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校九年級(1)班50名學生需要參加體育“五選一”自選項目測試,班上學生所報自選項目的情況統計如表所示:
自選項目 | 人數 | 頻率 |
立定跳遠 | b | 0.18 |
三級蛙跳 | 12 | 0.24 |
一分鐘跳繩 | 8 | a |
投擲實心球 | 16 | 0.32 |
推鉛球 | 5 | 0.10 |
合計 | 50 | 1 |
(1)求a,b的值;
(2)若該校九年級共有400名學生,試估計年級選擇“一分鐘跳繩”項目的總人數;
(3)在選報“推鉛球”的學生中,有3名男生,2名女生,為了了解學生的訓練效果,從這5名學生中隨機抽取兩名學生進行推鉛球測試,求所抽取的兩名學生中至少有一名女生的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,2×2網格(每個小正方形的邊長為1)中有A,B,C,D,E,F,G,H,O九個格點.拋物線l的解析式為y=(-1)nx2+bx+c(n為整數).

(1)n為奇數,且l經過點H(0,1)和C(2,1),求b,c的值,并直接寫出哪個格點是該拋物線上的頂點;
(2)n為偶數,且l經過點A(1, 0)和B(2,0),通過計算說明點F(0,2)和H(0,1)是否在拋物線上;
(3)若l經過這九個格點中的三個,直接寫出滿足這樣條件的拋物線條數.
查看答案和解析>>
科目:初中數學 來源: 題型:
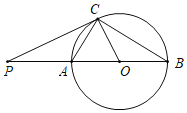
【題目】如圖,已知AB是⊙O的直徑,AC是弦,點P是BA延長線上一點,連接PC、BC,∠PCA=∠B.
(1)求證:PC是⊙O的切線;
(2)若PC=4,PA=2,求直徑AB的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
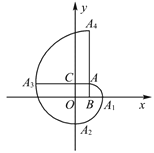
【題目】如圖,在平面直角坐標系中,四邊形![]() 是正方形,點
是正方形,點![]() 的坐標為
的坐標為![]() ,弧
,弧![]() 是以點
是以點![]() 為圓心,
為圓心,![]() 為半徑的圓弧;弧
為半徑的圓弧;弧![]() 是以點
是以點![]() 為圓心,
為圓心,![]() 為半徑的圓弧;弧
為半徑的圓弧;弧![]() 是以點
是以點![]() 為圓心,
為圓心,![]() 為半徑的圓弧;弧
為半徑的圓弧;弧![]() 是以點
是以點![]() 為圓心,
為圓心,![]() 為半徑的圓弧,繼續以點
為半徑的圓弧,繼續以點![]() 為圓心,按上述作法得到的曲線
為圓心,按上述作法得到的曲線![]() …,稱為正方形的“漸開線”,則點
…,稱為正方形的“漸開線”,則點![]() 的坐標是______.
的坐標是______.
查看答案和解析>>
科目:初中數學 來源: 題型:
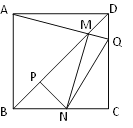
【題目】如圖,邊長一定的正方形ABCD,Q是CD上一動點,AQ交BD于點M,過M作MN⊥AQ交BC于N點,作NP⊥BD于點P,連接NQ,下列結論:①AM=MN;
②MP=![]() BD;③BN+DQ=NQ;④
BD;③BN+DQ=NQ;④![]() 為定值。其中一定成立的是_______.
為定值。其中一定成立的是_______.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com