
【題目】知識準備:數(shù)軸上![]() 兩點對應的數(shù)分別為
兩點對應的數(shù)分別為![]() .則
.則![]() 兩點之間的距離表示為:
兩點之間的距離表示為:![]()
問題探究:數(shù)軸上![]() 兩點對應的數(shù)分別為
兩點對應的數(shù)分別為![]() 且
且![]() 滿足
滿足![]()
![]() 直接寫出:
直接寫出:![]() ___、
___、![]()
![]() 在數(shù)軸上有一點
在數(shù)軸上有一點![]() 對應的數(shù)為
對應的數(shù)為![]() ,請問:當點
,請問:當點![]() 到
到![]() 兩點的距離和為
兩點的距離和為![]() 時,
時,![]() 滿足什么條件?請利用數(shù)軸進行說明(此時
滿足什么條件?請利用數(shù)軸進行說明(此時![]() 最小).
最小).
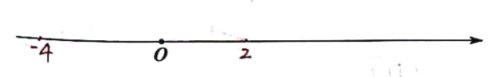
拓展:當數(shù)軸上 應用:國慶期間漢口江灘武漢關至長江二橋之間是觀看“70周年國慶燈光秀”的理想?yún)^(qū)域,武漢關與長江二橋相距約![]() 三點對應的數(shù)分別為
三點對應的數(shù)分別為![]() 在數(shù)軸上有一點
在數(shù)軸上有一點![]() 對應的數(shù)為
對應的數(shù)為![]() ,當
,當![]() 滿足什么條件時,
滿足什么條件時,![]() 的值最小?
的值最小? 
![]() 公里。在國慶期間,為了服務廣大市民,漢口江灘管理處在漢口江灘武漢關至長江二橋之間每隔
公里。在國慶期間,為了服務廣大市民,漢口江灘管理處在漢口江灘武漢關至長江二橋之間每隔![]() 公里安排了便民服務小組(武漢關與長江二橋不安排) ,還需要設置一個便民服務物資站,請問便民服務物資站應該設置在什么地方,使它到各個便民服務小組的距離和最小,最小值是多少公里?便民服務物資站位置代表的數(shù)記作
公里安排了便民服務小組(武漢關與長江二橋不安排) ,還需要設置一個便民服務物資站,請問便民服務物資站應該設置在什么地方,使它到各個便民服務小組的距離和最小,最小值是多少公里?便民服務物資站位置代表的數(shù)記作![]() 利用下圖直接給出結(jié)果:
利用下圖直接給出結(jié)果:![]() 滿足的條件: 最小值為 公里.
滿足的條件: 最小值為 公里.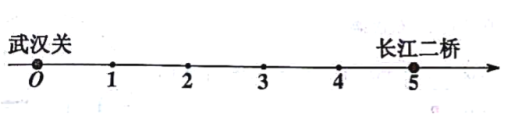
【答案】問題探究:(1)![]() ,
,![]() ; (2)
; (2)![]() ;拓展:當
;拓展:當![]() 時,
時,![]() 最小時為
最小時為![]() ;應用:
;應用:![]() ;4
;4
【解析】
問題探究:
(1)根據(jù)非負數(shù)的性質(zhì)可得![]() 和
和![]() 的值;
的值;
(2)根據(jù)絕對值的幾何意義,可得當點P在AB之間(包括A,B兩點),P到A點與P到B點的距離之和是6,即PA+PB最小;
拓展:點P在點A和點B(含點A和點B)之間,依此即可求解.
應用:同理根據(jù)拓展的問題,分情況即可求解.
問題探究:
(1)∵![]() .
.
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ;
;
故答案為:![]() ,
,![]() ;
;
(2)如圖1,

點P到A、B兩點的距離和為6時,點P在AB之間(包括A,B兩點),即![]() ,此時PA+PB最小;
,此時PA+PB最小;
拓展:

點P表示的數(shù)為2,該最小值為12,
設P到A、B、C的距離和為d,
則![]() ,
,
①當![]() 時,
時,![]() ,
,![]() 時,
時,![]() ;
;
②當![]() 時,
時,![]() ,
,![]() 時,
時,![]() ;
;
③當![]() 時,
時,![]() >12,
>12,
④當x>8時![]() >18;
>18;
綜上,當點P表示的數(shù)為2時,P到A、B、C的距離和最小,最小值為12.
應用:
如圖3,設便民服務物資站為點P,各便民服務小組分別為A,B,C,D,
設P到A、B、C、D的距離和為d,
則![]() ,
,
①當![]() 時,
時,![]() ,
,![]() 時,
時,![]() ;
;
②當![]() 時,
時,![]() >4,
>4,
③當![]() 時,
時,![]() ,
,
④當![]() 時,
時,![]() >4,
>4,
⑤當![]() 時,
時,![]() ,
,
當![]() 時,
時,![]() ;
;
綜上,![]() 滿足的條件:
滿足的條件:![]() ,最小值為4公里.
,最小值為4公里.
故答案為:![]() ,4.
,4.


 名校課堂系列答案
名校課堂系列答案科目:初中數(shù)學 來源: 題型:
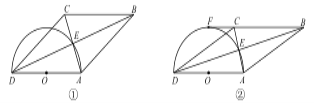
【題目】四邊形 ABCD 的對角線交于點 E,且 AE=EC,BE=ED,以 AD 為直徑的半圓過點 E,圓心 為 O.
(1)如圖①,求證:四邊形 ABCD 為菱形;
(2)如圖②,若 BC 的延長線與半圓相切于點 F,且直徑 AD=6,求弧AE 的長.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】小淇在說明 “直角三角形斜邊上的中線等于斜邊的一半”是真命題,部分思路如下:如圖,在∠ACB內(nèi)做∠BCD=∠B,CD與AB相交于點D,…….請根據(jù)以上思路,完成證明.

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】時代中學從學生興趣出發(fā),實施體育活動課走班制.為了了解學生最喜歡的一種球類運動,以便合理安排活動場地,在全校至少喜歡一種球類(乒乓球、羽毛球、排球、籃球、足球)運動的1200名學生中,隨機抽取了若干名學生進行調(diào)查(每人只能在這五種球類運動中選擇一種).調(diào)查結(jié)果統(tǒng)計如下:
球類名稱 | 乒乓球 | 羽毛球 | 排球 | 籃球 | 足球 |
人數(shù) | 42 |
| 15 | 33 |
|
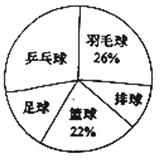
解答下列問題:
(1)這次抽樣調(diào)查中的樣本是________;
(2)統(tǒng)計表中,![]() ________,
________,![]() ________;
________;
(3)試估計上述1200名學生中最喜歡乒乓球運動的人數(shù).
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
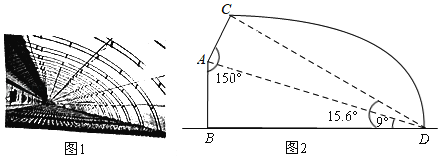
【題目】隨著我市農(nóng)產(chǎn)品整體品牌形象“聊勝一籌!”的推出,現(xiàn)代農(nóng)業(yè)得到了更快發(fā)展.某農(nóng)場為擴大生產(chǎn)建設了一批新型鋼管裝配式大棚,如圖1.線段AB,BD分別表示大棚的墻高和跨度,AC表示保溫板的長.已知墻高AB為2米,墻面與保溫板所成的角∠BAC=150°,在點D處測得A點、C點的仰角分別為9°,15.6°,如圖2.求保溫板AC的長是多少米?(精確到0.1米)
(參考數(shù)據(jù):![]() ≈0.86,sin9°≈0.16,cos9°≈0.99,tan9°≈0.16,sin15.6°≈0.27,cos15.6°≈0.96,tan15.6°≈0.28)
≈0.86,sin9°≈0.16,cos9°≈0.99,tan9°≈0.16,sin15.6°≈0.27,cos15.6°≈0.96,tan15.6°≈0.28)
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,已知拋物線![]() 與
與![]() 軸分別交于原點
軸分別交于原點![]() 和點
和點![]() ,與對稱軸
,與對稱軸![]() 交于點
交于點![]() .矩形
.矩形![]() 的邊
的邊![]() 在
在![]() 軸正半軸上,且
軸正半軸上,且![]() ,邊
,邊![]() ,
,![]() 與拋物線分別交于點
與拋物線分別交于點![]() ,
,![]() .當矩形
.當矩形![]() 沿
沿![]() 軸正方向平移,點
軸正方向平移,點![]() ,
,![]() 位于對稱軸
位于對稱軸![]() 的同側(cè)時,連接
的同側(cè)時,連接![]() ,此時,四邊形
,此時,四邊形![]() 的面積記為
的面積記為![]() ;點
;點![]() ,
,![]() 位于對稱軸
位于對稱軸![]() 的兩側(cè)時,連接
的兩側(cè)時,連接![]() ,
,![]() ,此時五邊形
,此時五邊形![]() 的面積記為
的面積記為![]() .將點
.將點![]() 與點
與點![]() 重合的位置作為矩形
重合的位置作為矩形![]() 平移的起點,設矩形
平移的起點,設矩形![]() 平移的長度為
平移的長度為![]() .
.
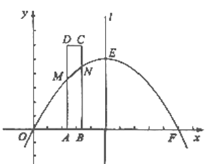
(1)求出這條拋物線的表達式;
(2)當![]() 時,求
時,求![]() 的值;
的值;
(3)當矩形![]() 沿著
沿著![]() 軸的正方向平移時,求
軸的正方向平移時,求![]() 關于
關于![]() 的函數(shù)表達式,并求出
的函數(shù)表達式,并求出![]() 為何值時,
為何值時,![]() 有最大值,最大值是多少?
有最大值,最大值是多少?
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】某校組織一項公益知識競賽,比賽規(guī)定:每個班級由2名男生、2名女生及1名班主任老師組成代表隊.但參賽時,每班只能有3名隊員上場參賽,班主任老師必須參加,另外2名隊員分別在2名男生和2名女生中各隨機抽出1名.初三(1)班由甲、乙2名男生和丙、丁2名女生及1名班主任組成了代表隊,求恰好抽到由男生甲、女生丙和這位班主任一起上場參賽的概率.(請用“畫樹狀圖”或“列表”或“列舉”等方法給出分析過程)
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,從邊長為a的大正方形中剪掉一個邊長為b的小正方形,將陰影部分剪下,拼成右邊的矩形,由圖形①到圖形②的變化過程能夠驗證的一個等式是( )
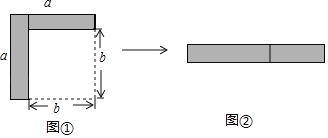
A. a(a+b)=a2+ab B. a2﹣b2=(a+b)(a﹣b)
C. (a+b)2=a2+2ab+b2 D. a(a﹣b)=a2﹣ab
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com