
【題目】 如圖,Rt△ABC 中,∠ACB=90 ,AC=6cm,BC=8cm,動點 P 從點 B 出發,在 BA邊上以每秒 5cm 的速度向點 A 勻速運動,同時動點 Q 從點 C 出發,在 CB 邊上以每秒 4cm 的 速度向點 B 勻速運動,運動時間為 t 秒(0<t<2),連接 PQ.
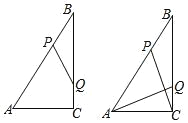
(1)若△BPQ 與△ABC 相似,求 t 的值;
(2)當 t 為何值時,四邊形 ACQP 的面積最小,最小值是多少?
(3)連接 AQ,CP,若 AQ⊥CP,求 t 的值。
【答案】(1) :當 t=1 或 t=![]() 時,△BPQ 與△ABC 相似;(2)18;(3) t=
時,△BPQ 與△ABC 相似;(2)18;(3) t=![]()
【解析】
根據題意△BPQ∽△BAC 相似再結合題意列比式解答此問,先四邊形 ACQP 的面積式用含t的表達式表示出來,再求其最小值;過點 P 作 PM⊥BC 于點 M,設 AQ 與 CP 相交于點 N,先證明△ACQ∽CMP,再利用結論求t值.
(1)①△BPQ∽△BAC 相似時,則![]()
∵BP=5t,QC=4t,AC=6cm,BC=8cm,
∴![]() ,解得:t=1;
,解得:t=1;
②△BPQ∽△BCA 相似時,
則![]() ,即
,即![]() ,解得:t=
,解得:t=![]()
綜合上述:當 t=1 或 t=![]() 時,△BPQ 與△ABC 相似,
時,△BPQ 與△ABC 相似,
(2)作 PM⊥BC 于點 M.則△BPM∽△BAC,
∴![]() ,即
,即![]() ,解得,PM=3t,
,解得,PM=3t,
設四邊形 ACQP 的面積為 y,由題意得:y=![]() ×6×8
×6×8![]() (84t)×3t=6(t1)2+18
(84t)×3t=6(t1)2+18
∴當 t=1 時,面積最小為 18.
(3)過點 P 作 PM⊥BC 于點 M,設 AQ 與 CP 相交于點 N,則有 PB=3t,MC=84t,
∵∠NAC+∠NCA=90 ,∠PCM+∠NCA=90 ,∴∠NAC=∠PCM, 又∵∠ACQ=∠CMP=90 ,∴△ACQ∽CMP,
∴![]() ,即
,即![]() ,解得:t=
,解得:t=![]()


 智慧課堂密卷100分單元過關檢測系列答案
智慧課堂密卷100分單元過關檢測系列答案 單元期中期末卷系列答案
單元期中期末卷系列答案科目:初中數學 來源: 題型:
【題目】隨著人們環保意識的不斷增強,我市家庭電動自行車的擁有量逐年增加.據統計,某小區2009年底擁有家庭電動自行車125輛,2011年底家庭電動自行車的擁有量達到180輛.
(1)若該小區2009年底到2012年底家庭電動自行車擁有量的年平均增長率相同,則該小區到2012年底電動自行車將達到多少輛?
(2)為了緩解停車矛盾,該小區決定投資3萬元再建若干個停車位,據測算,建造費用分別為室內車位1000元/個,露天車位200元/個.考慮到實際因素,計劃露天車位的數量不少于室內車位的2倍,但不超過室內車位的2.5倍,則該小區最多可建兩種車位各多少個?試寫出所有可能的方案.
查看答案和解析>>
科目:初中數學 來源: 題型:
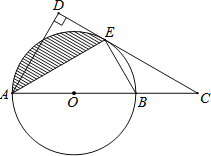
【題目】如圖,AB是⊙O的直徑,C是AB延長線上一點,CD與⊙O相切于點E,AD⊥CD于點D.
(1)求證:AE平分∠DAC;
(2)若AB=4,∠ABE=60°,求出圖中陰影部分的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
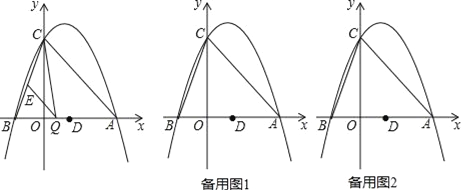
【題目】如圖,拋物線y=ax2﹣2ax+c(a≠0)與y軸交于點C(0,4),與x軸交于點A、B,點A坐標為(4,0).
(1)求該拋物線的解析式;
(2)拋物線的頂點為N,在x軸上找一點K,使CK+KN最小,并求出點K的坐標;
(3)點Q是線段AB上的動點,過點Q作QE∥AC,交BC于點E,連接CQ.當△CQE的面積最大時,求點Q的坐標;
(4)若平行于x軸的動直線l與該拋物線交于點P,與直線AC交于點F,點D的坐標為(2,0).問:是否存在這樣的直線l,使得△ODF是等腰三角形?若存在,請求出點P的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
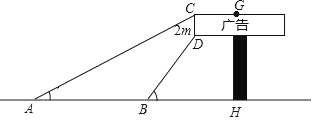
【題目】數學社團小組想利用所學的知識了解某廣告牌的高度(圖中GH的長),經測量知CD=2m,在B處測得點D的仰角為60°,在A處測得點C的仰角為30°,AB=10m,且A、B、H三點在一條直線上,請根據以上數據計算GH的長(![]() =1.73,要求結果精確得到0.1m)
=1.73,要求結果精確得到0.1m)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】二次函數![]() 的部分圖像如圖所示,圖像過點
的部分圖像如圖所示,圖像過點![]() ,對稱軸為直線
,對稱軸為直線![]() ,下列結論:(1)
,下列結論:(1)![]() ;(2)
;(2)![]() ;(3)若點
;(3)若點![]() 、點
、點![]() 、點
、點![]() 在該函數圖像上,則
在該函數圖像上,則![]() ;(4)若方程
;(4)若方程![]() 的兩根為
的兩根為![]() 和
和![]() ,且
,且![]() ,則
,則![]() .其中正確結論的序號是________.
.其中正確結論的序號是________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知關于x的一元二次方程x2﹣2x+m﹣1=0有兩個實數根x1,x2.
(1)求m的取值范圍;
(2)當x12+x22=6x1x2時,求m的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com