
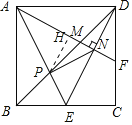
【題目】如圖,正方形ABCD的邊長為2,點E是BC的中點,AE與BD交于點P,F是CD上的一點,連接AF分別交BD,DE于點M,N,且AF⊥DE,連接PN,則下列結論中:

①![]() ;②
;②![]() ;③tan∠EAF=
;③tan∠EAF=![]() ;④
;④![]() 正確的是()
正確的是()
A. ①②③B. ①②④C. ①③④D. ②③④
【答案】A
【解析】
利用正方形的性質,得出∠DAN=∠EDC,CD=AD,∠C=∠ADF即可判定△ADF≌△DCE(ASA),再證明△ABM∽△FDM,即可解答①;根據題意可知:AF=DE=AE=![]() ,再根據三角函數即可得出③;作PH⊥AN于H.利用平行線的性質求出AH=
,再根據三角函數即可得出③;作PH⊥AN于H.利用平行線的性質求出AH=![]() ,即可解答②;利用相似三角形的判定定理,即可解答④
,即可解答②;利用相似三角形的判定定理,即可解答④
解:∵正方形ABCD的邊長為2,點E是BC的中點,
∴AB=BC=CD=AD=2,∠ABC=∠C=∠ADF=90°,CE=BE=1,
∵AF⊥DE,
∴∠DAF+∠ADN=∠ADN+∠CDE=90°,
∴∠DAN=∠EDC,
在△ADF與△DCE中, ,
,
∴△ADF≌△DCE(ASA),
∴DF=CE=1,
∵AB∥DF,
∴△ABM∽△FDM,
∴![]() ,
,
∴S△ABM=4S△FDM;故①正確;
根據題意可知:AF=DE=AE=![]() ,
,
∵![]() ×AD×DF=
×AD×DF=![]() ×AF×DN,
×AF×DN,
∴DN=![]() ,
,
∴EN=![]() ,AN=
,AN=![]() ,
,
∴tan∠EAF=![]() ,故③正確,
,故③正確,
作PH⊥AN于H.
∵BE∥AD,
∴![]() ,
,
∴PA=![]() ,
,
∵PH∥EN,
∴![]() ,
,
∴AH=![]() ,
,
∴PH=![]()
∴PN=![]() ,故②正確,
,故②正確,
∵PN≠DN,
∴∠DPN≠∠PDE,
∴△PMN與△DPE不相似,故④錯誤.
故選:A.


科目:初中數學 來源: 題型:
【題目】如圖,將拋物線![]() 平移后,新拋物線經過原拋物線的頂點
平移后,新拋物線經過原拋物線的頂點![]() ,新拋物線與
,新拋物線與![]() 軸正半軸交于點
軸正半軸交于點![]() ,聯結
,聯結![]() ,
,![]() ,設新拋物線與
,設新拋物線與![]() 軸的另一交點是
軸的另一交點是![]() ,新拋物線的頂點是
,新拋物線的頂點是![]() .
.
(1)求點![]() 的坐標;
的坐標;
(2)設點![]() 在新拋物線上,聯結
在新拋物線上,聯結![]() ,如果
,如果![]() 平分
平分![]() ,求點
,求點![]() 的坐標;
的坐標;
(3)在(2)的條件下,將拋物線![]() 沿
沿![]() 軸左右平移,點
軸左右平移,點![]() 的對應點為
的對應點為![]() ,當
,當![]() 和
和![]() 相似時,請直接寫出平移后得到拋物線的表達式.
相似時,請直接寫出平移后得到拋物線的表達式.
查看答案和解析>>
科目:初中數學 來源: 題型:
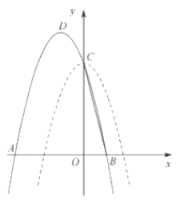
【題目】已知:拋物線![]() 與
與![]() 軸分別交于點A(-3,0),B(m,0).將y1向右平移4個單位得到y2.
軸分別交于點A(-3,0),B(m,0).將y1向右平移4個單位得到y2.
(1)求b的值;
(2)求拋物線y2的表達式;
(3)拋物線y2與![]() 軸交于點D,與
軸交于點D,與![]() 軸交于點E、F(點E在點F的左側),記拋物線在D、F之間的部分為圖象G(包含D、F兩點),若直線
軸交于點E、F(點E在點F的左側),記拋物線在D、F之間的部分為圖象G(包含D、F兩點),若直線![]() 與圖象G有一個公共點,請結合函數圖象,求直線
與圖象G有一個公共點,請結合函數圖象,求直線![]() 與拋物線y2的對稱軸交點的縱坐標t的值或取值范圍.
與拋物線y2的對稱軸交點的縱坐標t的值或取值范圍.

查看答案和解析>>
科目:初中數學 來源: 題型:
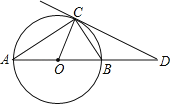
【題目】已知:如圖AB為⊙O直徑,C是⊙O上一點,D在AB的延長線上,∠DCB=∠A.
(1)求證:CD是⊙O的切線.
(2)若CD與⊙O相切,且∠D=30°,BD=10,求⊙O的半徑.
查看答案和解析>>
科目:初中數學 來源: 題型:
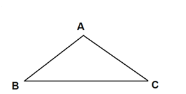
【題目】如圖,在△ABC中,AB=AC.
(1)若以點A為圓心的圓與邊BC相切于點D,請在下圖中作出點D;(要求:尺規作圖,不寫作法,保留作圖痕跡)
(2)在(1)的條件下,若該圓與邊AC相交于點E,連接DE,當∠BAC=100°時,求∠AED的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
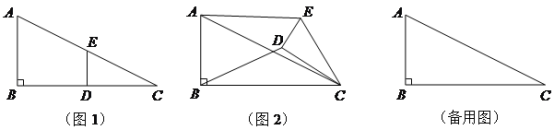
【題目】(10分)如圖1,在Rt△ABC中,∠B=90°,BC=2AB=8,點D,E分別是邊BC,AC的中點,連接DE. 將△EDC繞點C按順時針方向旋轉,記旋轉角為α.
(1)問題發現
① 當![]() 時,
時,![]() ;② 當
;② 當![]() 時,
時,![]()
(2)拓展探究
試判斷:當0°≤α<360°時,![]() 的大小有無變化?請僅就圖2的情況給出證明.
的大小有無變化?請僅就圖2的情況給出證明.
(3)問題解決
當△EDC旋轉至A、D、E三點共線時,直接寫出線段BD的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數y=-x2+bx+c(b,c為常數)的圖象經過點(2,3),(3,0).
(1)則b=,c=;
(2)該二次函數圖象與y軸的交點坐標為,頂點坐標為;
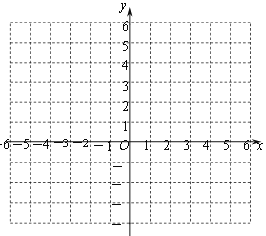
(3)在所給坐標系中畫出該二次函數的圖象;
(4)根據圖象,當-3<x<2時,y的取值范圍是.
查看答案和解析>>
科目:初中數學 來源: 題型:
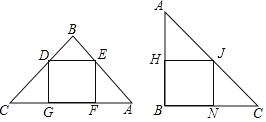
【題目】如圖一塊直角三角形ABC,∠B=90°,AB=3,BC=4,截得兩個正方形DEFG,BHJN,設S1=DEFG的面積,S2=BHJN的面積,則S1、S2的大小關系是( )
A.S1>S2B.S1<S2C.S1=S2D.不能確定
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com