【答案】
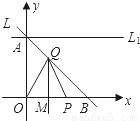
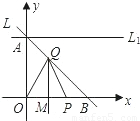
分析:(1)已知直線L過A,B兩點,可將兩點的坐標代入直線的解析式中,用待定系數法求出直線L的解析式;
(2)求三角形OPQ的面積,就需知道底邊OP和高QM的長,已知了OP為t,關鍵是求出QM的長.已知了QM垂直平分OP,那么OM=

t,然后要分情況討論:
①當OM<OB時,即0<t<2時,BM=OB-OM,然后在等腰直角三角形BQM中,即可得出QM=BM,由此可根據三角形的面積公式得出S與t的函數關系式.
②當OM>OB時,即當t≥2時,BM=OM-OB,然后根據①的方法即可得出S與t的函數關系式.
然后可根據0<t<2時的函數的性質求出S的最大值;
(3)如果存在這樣的點C,那么CQ=QP=OQ,因此C,O就關于直線BL對稱,因此C的坐標應該是(1,1).那么只需證明CQ⊥PQ即可.分三種情況進行討論.
①當Q在線段AB上(Q,B不重合),且P在線段OB上時.要證∠CQP=90°,那么在四邊形CQPB中,就需先證出∠QCB與∠QPB互補,由于∠QPB與∠QPO互補,而∠QPO=∠QOP,因此只需證∠QCB=∠QOB即可,根據折疊的性質,這兩個角相等,由此可得證.
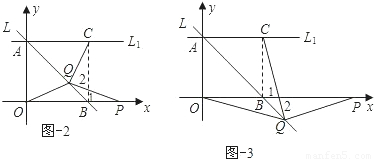
②當Q在線段AB上,P在OB的延長線上時,根據①已得出∠QPB=∠QCB,那么這兩個角都加上一個相等的對頂角后即可得出∠CQP=∠CBP=90度.
③當Q與B重合時,很顯然,三角形CQP應該是個等腰直角三角形.
綜上所述即可得出符合條件C點的坐標.
解答:解:由題意得
(1)y=1-x;
(2)∵OP=t,
∴Q點的橫坐標為

,
①當

,即0<t<2時,

,
∴S
△OPQ=

t(1-

t).
②當t≥2時,QM=|1-

t|=

t-1,
∴S
△OPQ=

t(

t-1).
∴
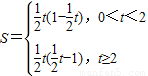
當0<

t<1,即0<t<2時,S=

t(1-

t)=-

(t-1)
2+

,
∴當t=1時,S有最大值

;
(3)由OA=OB=1,
所以△OAB是等腰直角三角形,
若在L
1上存在點C,使得△CPQ是以Q為直角頂點的等腰直角三角形,
則PQ=QC,
所以OQ=QC,又L
1∥x軸,則C,O兩點關于直線L對稱,
所以AC=OA=1,得C(1,1).下面證∠PQC=90度.連CB,則四邊形OACB是正方形.
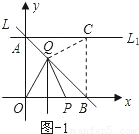
①當點P在線段OB上,Q在線段AB上(Q與B、C不重合)時,如圖-1.
由對稱性,得∠BCQ=∠QOP,∠QPO=∠QOP,
∴∠QPB+∠QCB=∠QPB+∠QPO=180°,
∴∠PQC=360°-(∠QPB+∠QCB+∠PBC)=90度.
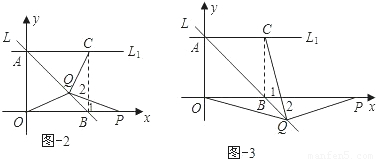
②當點P在線段OB的延長線上,Q在線段AB上時,如圖-2,如圖-3
∵∠QPB=∠QCB,∠1=∠2,
∴∠PQC=∠PBC=90度.
③當點Q與點B重合時,顯然∠PQC=90度.
綜合①②③,∠PQC=90度.
∴在L
1上存在點C(1,1),使得△CPQ是以Q為直角頂點的等腰直角三角形.
點評:本題結合了三角形的相關知識考查了一次函數及二次函數的應用,要注意的是(2)中為保證線段的長度不為負數要分情況進行求解.(3)中由于Q,P點的位置不確定,因此要分類進行討論不要漏解.


 t,然后要分情況討論:
t,然后要分情況討論:

 ,
, ,即0<t<2時,
,即0<t<2時, ,
, t(1-
t(1- t).
t). t|=
t|= t-1,
t-1, t(
t( t-1).
t-1).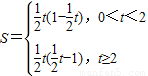
 t<1,即0<t<2時,S=
t<1,即0<t<2時,S= t(1-
t(1- t)=-
t)=- (t-1)2+
(t-1)2+ ,
, ;
;


 口算題天天練系列答案
口算題天天練系列答案