
【題目】如圖,AD、BE分別是△ABC的中線,AD、BE相交于點F. 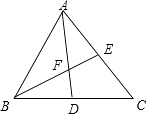
(1)△ABC與△ABD的面積有怎樣的數量關系?為什么?
(2)△BDF與△AEF的面積有怎樣的數量關系?為什么?
【答案】
(1)解:△ABC的面積是△ABD的面積的2倍.
理由:∵AD是△ABC的中線,
∴BD=CD,
又∵點A為△ABC的頂點,△ACD與△ABD同底等高,
∴△ACD的面積=△ABD的面積,
∴△ABC的面積是△ABD的面積的2倍

(2)解:△BDF與△AEF的面積相等.
理由:∵BE是△ABC的中線,
∴△ABC的面積是△ABE的面積的2倍,
又∵△ABC的面積是△ABD的面積的2倍,
∴△ABE的面積=△ABD的面積,
即△BDF的面積+△ABF的面積=△AEF的面積+△ABF的面積,
∴△BDF與△AEF的面積相等.
【解析】(1)根據三角形的中線將三角形分成面積相等的兩部分進行判斷;(2)根據三角形的中線將三角形分成面積相等的兩部分,得出△ABE的面積=△ABD的面積,再根據△BDF的面積+△ABF的面積=△AEF的面積+△ABF的面積,得出結論即可.
【考點精析】本題主要考查了三角形的“三線”和三角形的面積的相關知識點,需要掌握1、三角形角平分線的三條角平分線交于一點(交點在三角形內部,是三角形內切圓的圓心,稱為內心);2、三角形中線的三條中線線交于一點(交點在三角形內部,是三角形的幾何中心,稱為中心);3、三角形的高線是頂點到對邊的距離;注意:三角形的中線和角平分線都在三角形內;三角形的面積=1/2×底×高才能正確解答此題.


科目:初中數學 來源: 題型:
【題目】如圖,△ABC中,∠C=Rt∠,AB=5cm,BC=3cm,若動點P從點C開始,按C→A→B→C的路徑運動,且速度為每秒1cm,設出發的時間為t秒.
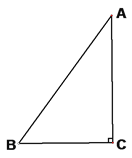
(1)出發2秒后,求△ABP的周長.
(2)問t滿足什么條件時,△BCP為直角三角形?
(3)另有一點Q,從點C開始,按C→B→A→C的路徑運動,且速度為每秒2cm,若P、Q兩點同時出發,當P、Q中有一點到達終點時,另一點也停止運動.當t為何值時,直線PQ把△ABC的周長分成相等的兩部分?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】正值重慶一中85年校慶之際,學校計劃利用校友慈善基金購買一些平板電腦和打印機.經市場調查,已知購買1臺平板電腦比購買3臺打印機多花費600元,購買2臺平板電腦和3臺打印機共需8400元.
(1)求購買1臺平板電腦和1臺打印機各需多少元?
(2)學校根據實際情況,決定購買平板電腦和打印機共100臺,要求購買的總費用不超過168000元,且購買打印機的臺數不低于購買平板電腦臺數的2倍.請問最多能購買平板電腦多少臺?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知四邊形ABCD為菱形,連接BD,點E為菱形ABCD外任一點.
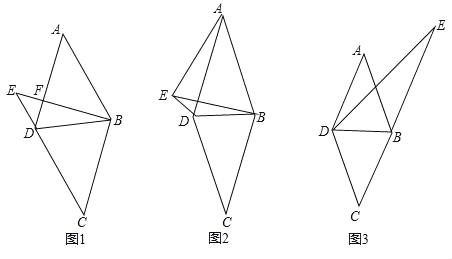
(1)如圖(1),若∠A=45°,AB=![]() ,點E為過點B作AD邊的垂線與CD邊的延長線的交點,BE,AD交于點F,求DE的長.
,點E為過點B作AD邊的垂線與CD邊的延長線的交點,BE,AD交于點F,求DE的長.
(2)如圖(2),若2∠AEB=180°﹣∠BED,∠ABE=60°,求證:BC=BE+DE
(3)如圖(3),若點E在的CB延長線上時,連接DE,試猜想∠BED,∠ABD,∠CDE三個角之間的數量關系,直接寫出結論
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數y=ax2+bx+c(a≠0)的圖象如圖所示,下列結論:①2a+b<0;②abc>0;③4a﹣2b+c>0;④a+c>0,其中正確結論的個數為( ).

A.4個 B.3個 C.2個 D.1個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】計算或化簡:
(1)(﹣1)2015﹣2﹣1+(π﹣3.14)0
(2)a3﹒a3+(﹣2a3)2﹣a8÷a2
(3)﹣5x(﹣x2+2x+1)﹣(2x﹣3)(5+x2)
(4)(x+3y﹣4z)(x﹣3y+4z)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在下列調查中,適宜采用普查的是( )
A.了解某校九(1)班學生視力情況B.調查2020年央視春晚的收視率
C.檢測一批電燈泡的使用壽命D.了解我市中學生課余上網時間
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com