
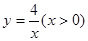 經過四邊形OABC的頂點A、C,∠ABC=90°,OC平分OA與
經過四邊形OABC的頂點A、C,∠ABC=90°,OC平分OA與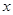 軸正半軸的夾角 ,AB∥
軸正半軸的夾角 ,AB∥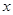 軸,將△ABC翻折后,得△
軸,將△ABC翻折后,得△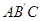 ,
,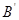 點落在OA上,則四邊形OABC的面積為 .
點落在OA上,則四邊形OABC的面積為 .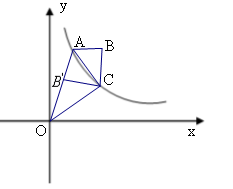
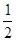 xy,則S△OCB′=
xy,則S△OCB′=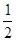 xy,由AB∥x軸,得點A(x-a,2y),由題意得2y(x-a)=6,從而得出三角形ABC的面積等于
xy,由AB∥x軸,得點A(x-a,2y),由題意得2y(x-a)=6,從而得出三角形ABC的面積等于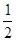 ay,即可得出答案.
ay,即可得出答案.
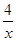 (x>0)經過四邊形OABC的頂點A、C,
(x>0)經過四邊形OABC的頂點A、C,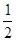 xy=2,
xy=2,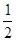 xy=2,
xy=2,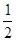 ay=1,
ay=1,

科目:初中數學 來源:不詳 題型:單選題
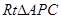 的頂點A,P在反比例函數
的頂點A,P在反比例函數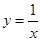 的圖像上,已知P的坐標為(1,1),
的圖像上,已知P的坐標為(1,1),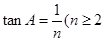 的自然數);當n=2,3,4…2010時,A的橫坐標相應為
的自然數);當n=2,3,4…2010時,A的橫坐標相應為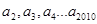 ,則
,則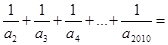 ( )
( )A.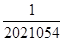 | B.2021054 | C.2022060 | D.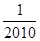 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com