【題目】下圖是某同學在沙灘上用石子擺成的小房子．觀察圖形的變化規律，第6個小房子用的石子數量為 ( )
A. 87 B. 77 C. 70 D. 60
【答案】D
【解析】要找這個小房子的規律，可以分為兩部分來看：第一個屋頂是1，第二個屋頂是3．第三個屋頂是5．以此類推，第n個屋頂是2n-1．第一個下邊是4．第二個下邊是9．第三個下邊是16．以此類推，第n個下邊是（n+1）2個．兩部分相加即可得出第n個小房子用的石子數是（n+1）2+2n-1=n2+4n，將n=7代入求值即可．
該小房子用的石子數可以分兩部分找規律：
屋頂：第一個是1，第二個是3，第三個是5，…，以此類推，第n個是2n-1；
下邊：第一個是4，第二個是9，第三個是16，…，以此類推，第n個是（n+1）2個．
所以共有（n+1）2+2n-1=n2+4n．
當n=6時，
n2+4n=60，
故選：D．
科目：初中數學 來源： 題型：
【題目】為了了解全校2400名學生的閱讀興趣，從中隨機抽查了部分同學，就“我最感興趣的書籍”進行了調查：A.小說、B.散文、C.科普、D.其他（每個同學只能選擇一項），進行了相關統計，整理并繪制出兩幅不完整的統計圖，請你根據統計圖提供的信息，解答下列問題：
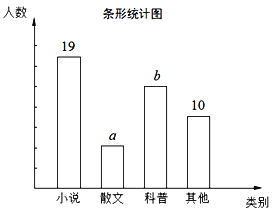
（1）本次抽查中，樣本容量為______；
（2）a＝______，b＝______；
（3）扇形統計圖中，其他類書籍所在扇形的圓心角是______°；
（4）請根據樣本數據，估計全校有多少名學生對散文感興趣．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在矩形ABCD中 ,AB=4，BC=8，點E為CD中點，P、Q為BC邊上兩個動點，且PQ=2，當四邊形APQE周長最小時，BP的長為（ ）
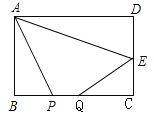
A. 1 B. 2 C. 2
D. 4
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，點A、B都在數軸上，O為原點．
（1）點B表示的數是_________________；
（2）若點B以每秒2個單位長度的速度沿數軸向右運動，則2秒后點B表示的數是________；
（3）若點A、B分別以每秒1個單位長度、3個單位長度的速度沿數軸向右運動，而點O不動，t秒后，A、B、O三個點中有一個點是另外兩個點為端點的線段的中點，求t的值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知在紙面上有一數軸（如圖），折疊紙面．例如：若數軸上數2表示的點與數﹣2表示的點重合，則數軸上數﹣4表示的點與數4表示的點重合，根據你對例題的理解，解答下列問題：
若數軸上數﹣3表示的點與數1表示的點重合．（根據此情境解決下列問題）
①則數軸上數3表示的點與數 表示的點重合．
②若點A到原點的距離是5個單位長度，并且A、B兩點經折疊后重合，則B點表示的數是 ．
③若數軸上M、N兩點之間的距離為2018，并且M、N兩點經折疊后重合，
如果M點表示的數比N點表示的數大，則M點表示的數是 ．則N點表示的數是 ．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】a
b是新規定的一種運算法則：ab=a2+ab，例如3（﹣2）=32+3×（﹣2）=3．
（1）求（﹣3）5的值；
（2）若（﹣2）x=6，求x的值；
（3）若3（2x）=﹣4+x，求x的值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】列一元一次方程解應用題．
（1）商店出售茶壺和茶杯，茶壺每只定價20元，茶杯每只定價5元，該商品制定了兩種優惠方法：
①買一只茶壺贈一只茶杯；②按總價的90%付款．某顧客購買茶壺5只，茶杯若干只（不少于5只），問顧客買多少只茶杯時，兩種方法付款相同．假如該顧客買了茶杯20只，哪種買法實惠？
（2）某人原計劃騎車以每小時12千米的速度由A地到B地，這樣便可在規定的時間到達，但他因事將原計劃出發的時間推遲了20分鐘，只好以每小時15千米的速度前進，結果比規定時間早4分鐘到達B地，求A，B兩地間的距離．
（3）某工廠完成一批產品，一車間單獨完成需30天，二車間單獨完成需20天．
①如一車間先做若干天，然后由二車間繼續做，直至完成，前后共做了25天，問一車間先做了幾天？
②如一車間先做了3天后，二車間加入一起做，還需多少天才能完成？
查看答案和解析>>
科目：初中數學 來源： 題型：
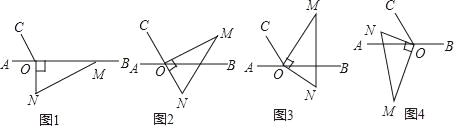
【題目】如圖，已知點O為直線AB上一點，將一直角三角板的直角頂點放在點O處．
（1）如圖1，將三角板的一邊ON與射線OB重合，過點O在三角板的內部，作射線OC，使∠NOC：∠MOC=2：1，求∠AOC的度數；
（2）如圖2，將三角板繞點O逆時針旋轉一定角度到圖2的位置，過點O在三角板MON的內部作射線OC，使得OC恰好是∠MOB對的角平分線，此時∠AOM與∠NOC滿足怎樣的數量關系？并說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖1，點O為直線AB上一點，過點O作射線OC，使∠AOC=60°，將一把直角三角尺的直角頂點放在點O處，一邊OM在射線OB上，另一邊ON在直線AB的下方．
（1）將圖1中的三角尺繞點O逆時針旋轉至圖2，使點N在OC的反向延長線上，請直接寫出圖中∠MOB的度數；
（2）將圖1中的三角尺繞點O逆時針旋轉至圖3，使一邊OM在∠BOC的內部，且恰好平分∠BOC，求∠CON的度數；
（3）將圖1中的三角尺繞點O順時針旋轉至圖4，使ON在∠AOC的內部，請探究∠AOM與∠NOC之間的數量關系，并說明理由．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com