【題目】為了說明命題“等腰三角形腰上的高小于腰”是假命題，可以找的反例是_____．
科目：初中數學 來源： 題型：
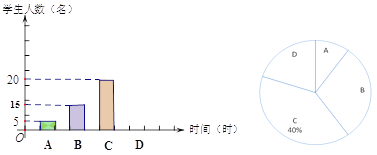
【題目】某校在九年級學生中開展以“每天數學家庭作業完成時間”設置的一個問題，有以下選項：
A.0～0.5小時B.0.5～1個小時 C.1個小時～1.5個小時 D.1.5個小時以上
在隨機調查了九（1）班學生后，根據相關數據給出如圖所示的統計圖．
（1）該校九（1）班學生 人；做數學家庭作業1.5個小時以上的占 ；
（2）補全頻數直方圖；
（3）已知該校九年級共400名學生，據此推算，該校九年級學生中，“做數學家庭作業1.5個小時以上”的學生人數.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知如圖，在數軸上點
， 
所對應的數是
， 
．
對于關于
的代數式
，我們規定：當有理數
在數軸上所對應的點為
之間（包括點
， 
）的任意一點時，代數式
取得所有值的最大值小于等于
，最小值大于等于
，則稱代數式
，是線段
的封閉代數式．
例如，對于關于
的代數式
，當
時，代數式
取得最大值是
；當
時，代數式
取得最小值是
，所以代數式
是線段
的封閉代數式．
問題：（
）關于
代數式
，當有理數
在數軸上所對應的點為
之間（包括點
， 
）的任意一點時，取得的最大值和最小值分別是__________．
所以代數式
__________（填是或不是）線段
的封閉代數式．
（
）以下關
的代數式：
①
；②
；③
；④
．
是線段
的封閉代數式是__________，并證明（只需要證明是線段
的封閉代數式的式子，不是的不需證明）．
（
）關于
的代數式
是線段
的封閉代數式，則有理數
的最大值是__________，最小值是__________．
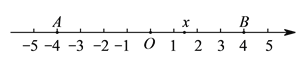
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在平面直角坐標系xOy中，直線y=kx+2與x軸、y軸分別交于點A(-1,0)和點B，與反比例函數y=
的圖象在第一象限內交于點C（1，n）．
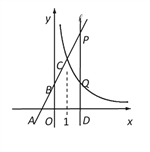
（1）求k的值；
（2）求反比例函數的解析式；
（3）過x軸上的點D（a，0）作平行于y軸的直線
（a＞1），分別與直線AB和雙曲線
交于點P、Q，且PQ=2QD，求點D的坐標．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，四邊形ABCD是矩形，DG平分∠ADB交AB于點G，GF⊥BD于F．
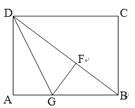
（1）求證：△ADG≌△FDG；（2）若BG=2AG，BD=2
，求AD的長.
查看答案和解析>>
科目：初中數學 來源： 題型：
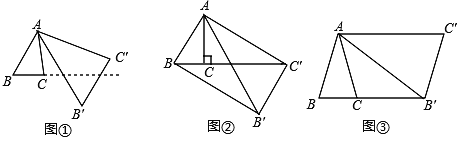
【題目】將△ABC繞點A按逆時針方向旋轉θ度，并使各邊長變為原來的n倍，得△AB′C′ ，如圖①所示，∠BAB′ ＝θ， 
，我們將這種變換記為[θ，n] ．
（1）如圖①，對△ABC作變換[60°，
]得到△AB′C′ ，則
:
= ；直線BC與直線B′C′所夾的銳角為 度；
（2）如圖②，△ABC中，∠BAC=30°，∠ACB=90°，對△ABC作變換[θ，n]得到△AB′C′，使點B、C、
在同一直線上，且四邊形ABB′C′為矩形，求θ和n的值；
（3）如圖③，△ABC中，AB=AC，∠BAC=36°，BC=1，對△ABC作變換[θ，n]得到△AB′C′，使點B、C、B′在同一直線上，且四邊形ABB′C′為平行四邊形，求θ和n的值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，一次函數y=mx+4的圖象與x軸相交于點A，與反比例函數y=
的圖象相交于點B（1，6）．
（1）求一次函數和反比例函數的解析式；
（2）設點P是x軸上一點，若S△APB=18，直接寫出點P的坐標．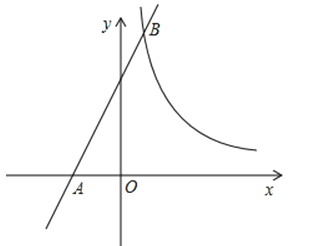
查看答案和解析>>
科目：初中數學 來源： 題型：
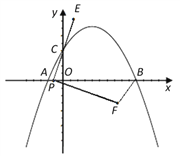
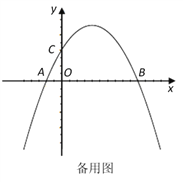
【題目】如圖，在平面直角坐標系中，已知點A、B、C的坐標分別為(-1，0)，(5，0)，(0，2)．
（1）求過A、B、C三點的拋物線解析式；
（2）若點P從A點出發，沿x軸正方向以每秒1個單位長度的速度向B點移動，連接PC并延長到點E，使CE=PC，將線段PE繞點P順時針旋轉90°得到線段PF，連接FB．若點P運動的時間為t秒(0≤t≤6)，設△PBF的面積為S；
①求S與t的函數關系式；
②當t是多少時，△PBF的面積最大，最大面積是多少？
（3）點P在移動的過程中，△PBF能否成為直角三角形？若能，直接寫出點F的坐標；若不能，請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知反比例函數y=
（m為常數）的圖象在一，三象限．
（1）求m的取值范圍；
（2）如圖，若該反比例函數的圖象經過ABOD的頂點D，點A、B的坐標分別為（0，4），（﹣3，0）．
①求出函數解析式；
②設點P是該反比例函數圖象上的一點，若OD=OP，則P點的坐標為多少？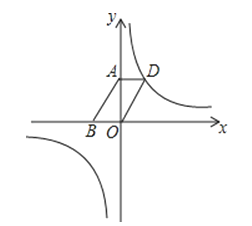
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
