
【題目】如圖,△ABC是等邊三角形,D是AB邊上一點,以CD為邊作等邊三角形CDE,使點E,A在直線DC同側,連接AE.求證:

(1)△AEC≌BDC;
(2)AE∥BC.
【答案】見解析
【解析】
試題分析:(1)根據等邊三角形性質推出BC=AC,CD=CE,∠BCA=∠ECD=60°,求出∠BCD=∠ACE,根據SAS證△AEC≌△BDC;
(2)根據△AEC≌△BDC推出∠EAC=∠DBC=∠ACB,根據平行線的判定推出即可.
解:(1)∵△ABC和△DEC是等邊三角形,
∴BC=AC,CD=CE,∠BCA=∠ECD=60°,∠B=60°,
∴∠BCA﹣∠DCA=∠ECD﹣∠DCA,
即∠BCD=∠ACE,
在△AEC和△BDC中,
 ,
,
∴△AEC≌△BDC(SAS).
(2)∵△AEC≌△BDC,
∴∠EAC=∠B,
∵∠B=60°,
∴∠EAC=∠B=60°=∠ACB,
∴AE∥BC.


 中考解讀考點精練系列答案
中考解讀考點精練系列答案科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AD⊥BC且BD>CD,DF⊥AB,△CDE和△ADB都是等腰直角三角形,給出下列結論,正確的是
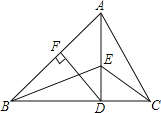
①△ADC≌△BDE;
②△ADF≌△BDF;
③△CDE≌△AFD;
④△ACE≌ABE.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】
![]()
(1)寫出A、B兩點所表示的數,并求線段AB的長;
(2)將點A向左移動![]() 個單位長度得到點C,點C表示的數是多少,并在數軸上表示出來
個單位長度得到點C,點C表示的數是多少,并在數軸上表示出來
(3)數軸上存在一點D,使得C、D兩點間的距離為8,請寫出D點表示的數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在一個不透明的口袋中,放有三個標號分別為1,2,3的質地、大小都相同的小球.任意摸出一個小球,記為x,再從剩余的球中任意摸出一個小球,又記為y,得到點(x,y).
(1)用畫樹狀圖或列表等方法求出點(x,y)的所有可能情況;
(2)求點(x,y)在二次函數y=ax2﹣4ax+c(a≠0)圖象的對稱軸上的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某中學了解本校學生對球類運動的愛好情況,分為足球、籃球、排球、其他四個方面調查若干名學生,每人只選其中之一,統計后繪制成不完整的“折線統計圖”(扇形統計圖),根據信息解答下列問題:
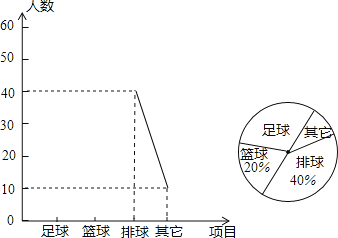
(1)在這次調查中,一共調查 名學生;
(2)在扇形統計圖中,“足球”所在扇形圓心角 度;
(3)將折線統計圖補充完整.
查看答案和解析>>
科目:初中數學 來源: 題型:
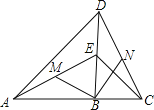
【題目】如圖,已知點B在線段AC上,點E在線段BD上,∠ABD=∠DBC,AB=DB,EB=CB,M,N分別是AE,CD的中點,現有如下結論:①∠ABD=∠BDN;②MB=NB;③MB⊥NB;④S△ABM=S△BCN,其中正確的結論是 (只填序號).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知△ABC的三個頂點的坐標為:A(2,4),B(4,3),C(1,1),直線l過點(﹣1,0)且平行于y軸.
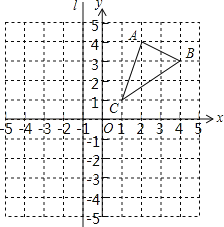
(1)在圖中作出△ABC關于x軸對稱的△A′B′C′;
(2)作出△ABC關于直線l對稱的△A1B1C1,并寫出△A1B1C1三個頂點的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】計算
(1) ![]() (2) 12+(-8)+11+(-2)+(-12)
(2) 12+(-8)+11+(-2)+(-12)
![]() +
+![]() (4) (-24)÷2×(-3)÷(-6)
(4) (-24)÷2×(-3)÷(-6)
(5)![]() (6)(-4)×(-2
(6)(-4)×(-2![]() )+(-8)×(-2
)+(-8)×(-2![]() )+12×(-2
)+12×(-2![]() )
)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com