
【題目】如圖,在平面直角坐標系中,已知點A、B、C的坐標分別為(﹣1,0),(5,0),(0,2).若點P從A點出發,沿x軸正方向以每秒1個單位長度的速度向B點移動,連接PC并延長到點E,使CE=PC,將線段PE繞點P順時針旋轉90°得到線段PF,連接FB.若點P在移動的過程中,使△PBF成為直角三角形,則點F的坐標是 . 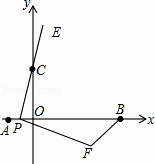
【答案】(5,2),( ![]() ,
, ![]() )
)
【解析】解:能;
①若F為直角頂點,過F作FD⊥x軸于D,則BP=6﹣t,DP=2OC=4,
在Rt△OCP中,OP=t﹣1,
由勾股定理易求得CP2=t2﹣2t+5,那么PF2=(2CP)2=4(t2﹣2t+5);
在Rt△PFB中,FD⊥PB,
由射影定理可求得PB=PF2÷PD=t2﹣2t+5,
而PB的另一個表達式為:PB=6﹣t,
聯立兩式可得t2﹣2t+5=6﹣t,即t= ![]() ,
,
P點坐標為( ![]() ,0),
,0),
則F點坐標為:( ![]() ,
, ![]() );
);
②B為直角頂點,那么此時的情況與①題類似,△PFB∽△CPO,且相似比為2,
那么BP=2OC=4,即OP=OB﹣BP=1,此時t=2,
P點坐標為(1,0).FD=2(t﹣1)=2,
則F點坐標為(5,2).
故答案是:(5,2),( ![]() ,
, ![]() ).
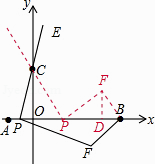
).
【考點精析】根據題目的已知條件,利用圖形的旋轉的相關知識可以得到問題的答案,需要掌握每一個點都繞旋轉中心沿相同方向轉動了相同的角度,任意一對對應點與旋轉中心的連線所成的角都是旋轉角,對應點到旋轉中心的距離相等.旋轉的方向、角度、旋轉中心是它的三要素.


科目:初中數學 來源: 題型:
【題目】已知:如圖,在Rt△ABC中,∠C=90°,BD平分∠ABC,交AC于點D,經過B、D兩點的⊙O交AB 于點E,交BC于點F,EB為⊙O的直徑. 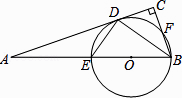
(1)求證:AC是⊙O的切線;
(2)當BC=2,cos∠ABC= ![]() 時,求⊙O的半徑.
時,求⊙O的半徑.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某市為了構建城市立體道路網絡,決定修建一條輕軌鐵路,為使工程提前半年完成,需要將工作效率提高25%,原計劃完成這項工程需要多少個月?
【答案】原計劃完成這項工程需要30個月
【解析】試題設原計劃完成這項工程需要x個月,由等量關系“工程提前6個月完成,需將原定的工作效率提高25%”列出方程,求解即可
試題解析:設原計劃完成這項工程需要x個月,則有
![]()
解得x=30
經檢驗x=30是原方程的根
答:原計劃完成這項工程需要30個月
考點:分式方程的應用
【題型】解答題
【結束】
24
【題目】如圖,一次函數![]() 分別交y軸、x軸于C、D兩點,與反比例函數y=
分別交y軸、x軸于C、D兩點,與反比例函數y=![]() (x>0)的圖象交于A(m,8),B(4,n)兩點.
(x>0)的圖象交于A(m,8),B(4,n)兩點.
(1)求反比例函數的解析式;
(2)根據圖象直接寫出![]() <
<![]() 的x的取值范圍;
的x的取值范圍;
(3)求![]() 的面積.
的面積.
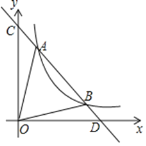
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某工程交由甲、乙兩個工程隊來完成,已知甲工程隊單獨完成需要60天,乙工程隊單獨完成需要40天
(1)若甲工程隊先做30天后,剩余由乙工程隊來完成,還需要用時 天
(2)若甲工程隊先做20天,乙工程隊再參加,兩個工程隊一起來完成剩余的工程,求共需多少天完成該工程任務?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知關于x的方程(a+2)x2﹣2ax+a=0有兩個不相等的實數根x1和x2 , 拋物線y=x2﹣(2a+1)x+2a﹣5與x軸的兩個交點分別為位于點(2,0)的兩旁,若|x1|+|x2|=2 ![]() ,則a的值為 .
,則a的值為 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某公司在某市五個區投放共享單車供市民使用,投放量的分布及投放后的使用情況統計如下.
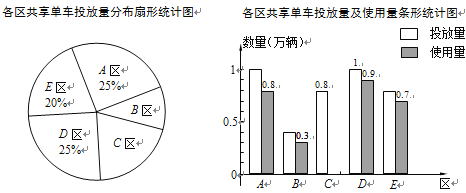
(1)該公司在全市一共投放了 萬輛共享單車;
(2)在扇形統計圖中,B區所對應扇形的圓心角為 °;
(3)該公司在全市投放的共享單車的使用量占投放量的85%,請計算C區共享單車的使用量并補全條形統計圖.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知數軸上的點A表示的數為6,點B表示的數為﹣4,點C到點A、點B的距離相等,動點P從點B出發,以每秒2個單位長度的速度沿數軸向右勻速運動,設運動時間為x(x大于0)秒.
(1)點C表示的數是 ;
(2)當x= 秒時,點P到達點A處?
(3)運動過程中點P表示的數是 (用含字母x的式子表示);
(4)當P,C之間的距離為2個單位長度時,求x的值.
![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線的對稱軸是x=1,與x軸有兩個交點,與y軸的交點坐標是(0,3),把它向下平移2個單位長度后,得到新的拋物線的解析式是y=ax2+bx+c,以下四個結論: ①b2﹣4ac<0,②abc<0,③4a+2b+c=1,④a﹣b+c>0中,其中正確的是(填序號).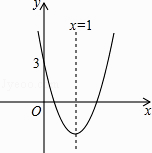
查看答案和解析>>
科目:初中數學 來源: 題型:
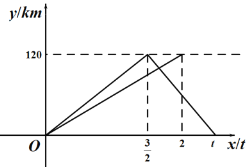
【題目】一輛轎車從甲地駛往乙地,到達乙地后立即返回甲地,速度是原來的1.5倍,往返共用t小時.一輛貨車同時從甲地駛往乙地,到達乙地后停止.兩車同時出發,勻速行駛,設轎車行駛的時間為x(h),兩車離開甲地的距離為y(km),兩車行駛過程中y與x之間的函數圖象如圖所示.
(1)轎車從乙地返回甲地的速度為 km/t,t= h;
(2)求轎車從乙地返回甲地時y與x之間的函數關系式;
(3)當轎車從甲地返回乙地的途中與貨車相遇時,求相遇處到甲地的距離.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com