
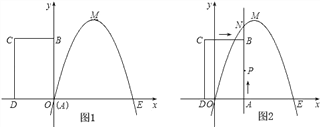
【題目】如圖,已知拋物線經過坐標原點O和x軸上另一點E,頂點M的坐標為(2,4);矩形ABCD的頂點A與點O重合,AD、AB分別在x軸、y軸上,且AD=2,AB=3.
(1)求該拋物線所對應的函數關系式;
(2)將矩形ABCD以每秒1個單位長度的速度從如圖所示的位置沿x軸的正方向勻速平行移動,同時一動點P也以相同的速度從點A出發向B勻速移動,設它們運動的時間為t秒(0≤t≤3),直線AB與該拋物線的交點為N(如圖2所示).
①當t=![]() 時,判斷點P是否在直線ME上,并說明理由;
時,判斷點P是否在直線ME上,并說明理由;
②設以P、N、C、D為頂點的多邊形面積為S,試問S是否存在最大值?若存在,求出這個最大值;若不存在,請說明理由.
【答案】(1) y=﹣x2+4x;(2) ①點P不在直線ME上,理由見解析;②S存在最大值,理由見解析.
【解析】分析:(1)設出拋物線的頂點式y=a(x-2)2+4,將原點的坐標代入解析式就可以求出a的值,從而求出函數的解析式.
(2)①由(1)中拋物線的解析式可以求出E點的坐標,從而可以求出ME的解析式,再將P點的坐標代入直線的解析式就可以判斷P點是否在直線ME上.
②設出點N(t,-(t-2)2+4),可以表示出PN的值,根據梯形的面積公式可以表示出S與t的函數關系式,從而可以求出結論.
詳解:(1)因所求拋物線的頂點M的坐標為(2,4),
故可設其關系式為y=a(x﹣2)2+4
又∵拋物線經過O(0,0),
∴得a(0﹣2)2+4=0,
解得a=﹣1
∴所求函數關系式為y=﹣(x﹣2)2+4,
即y=﹣x2+4x.
(2)①點P不在直線ME上.
根據拋物線的對稱性可知E點的坐標為(4,0),
又M的坐標為(2,4),
設直線ME的關系式為y=kx+b.
于是得![]() ,
,
解得![]()
所以直線ME的關系式為y=﹣2x+8.
由已知條件易得,當t=![]() 時,OA=AP=
時,OA=AP=![]() ,
,
∴P(![]() ,
,![]() )
)
∵P點的坐標不滿足直線ME的關系式y=﹣2x+8.
∴當t=![]() 時,點P不在直線ME上.
時,點P不在直線ME上.
②S存在最大值.理由如下:
∵點A在x軸的非負半軸上,且N在拋物線上,
∴OA=AP=t.
∴點P,N的坐標分別為(t,t)、(t,﹣t2+4t)
∴AN=﹣t2+4t(0≤t≤3),
∴AN﹣AP=(﹣t2+4t)﹣t=﹣t2+3t=t(3﹣t)≥0,
∴PN=﹣t2+3t
(ⅰ)當PN=0,即t=0或t=3時,以點P,N,C,D為頂點的多邊形是三角形,此三角形的高為AD,
∴S=![]() DCAD=
DCAD=![]() ×3×2=3.
×3×2=3.
(ⅱ)當PN≠0時,以點P,N,C,D為頂點的多邊形是四邊形
∵PN∥CD,AD⊥CD,
∴S=![]() (CD+PN)AD=
(CD+PN)AD=![]() [3+(﹣t2+3t)]×2=﹣t2+3t+3=﹣(t﹣
[3+(﹣t2+3t)]×2=﹣t2+3t+3=﹣(t﹣![]() )2+
)2+![]()
其中(0<t<3),由a=﹣1,0<![]() <3,此時S最大=
<3,此時S最大=![]() .
.
綜上所述,當t=![]() 時,以點P,N,C,D為頂點的多邊形面積有最大值,這個最大值為
時,以點P,N,C,D為頂點的多邊形面積有最大值,這個最大值為![]() .
.
說明:(ⅱ)中的關系式,當t=0和t=3時也適合.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
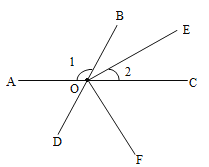
【題目】如圖所示,點![]() 、
、![]() 、
、![]() 在同一直線上,
在同一直線上,![]() 是
是![]() 的平分線,
的平分線,![]() ,
,![]() ,
,![]() .
.
(1)求![]() 的度數(請寫出解題過程).
的度數(請寫出解題過程).
(2)如以![]() 為一邊,在
為一邊,在![]() 的外部畫
的外部畫![]() ,問邊
,問邊![]() 與邊
與邊![]() 成一直線嗎?請說明理由.
成一直線嗎?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
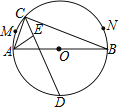
【題目】如圖,![]() 是
是![]() 的直徑,
的直徑,![]() 、
、![]() 是弧
是弧![]() (異于
(異于![]() 、
、![]() )上兩點,
)上兩點,![]() 是弧
是弧![]() 上一動點,
上一動點,![]() 的角平分線交
的角平分線交![]() 于點
于點![]() ,
,![]() 的平分線交
的平分線交![]() 于點
于點![]() .當點
.當點![]() 從點
從點![]() 運動到點
運動到點![]() 時,則
時,則![]() 、
、![]() 兩點的運動路徑長的比是( )
兩點的運動路徑長的比是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】對于有理數a, b,規定一種新運算: a★b= 2ab-b.
(1)計算: (-3)★4=______________;
(2)若方程(x-4)★3=6,求x的值;
(3)計算: 5★[(-2)★3]的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】對于一次函數![]()
![]() ,我們稱函數
,我們稱函數![]()
![]()
為它的m分函數(其中m為常數).
例如,![]() 的4分函數為:當
的4分函數為:當![]() 時,
時,![]() ;當
;當![]() 時,
時,![]() .
.
(1)如果![]() 的2分函數為
的2分函數為![]() ,
,
① 當![]() 時,
時,![]() ; ②當
; ②當![]() 時,
時,![]() .
.
(2)如果![]() 的-1分函數為
的-1分函數為![]() ,求雙曲線
,求雙曲線![]() 與
與![]() 的圖象的交點坐標;
的圖象的交點坐標;
(3)從下面兩問中任選一問作答:
①設y=x+2的m分函數為y![]() ,如果拋物線y=x
,如果拋物線y=x![]() 與y
與y![]() 的圖象有且只有一個公共點,直接寫出m的取值范圍。
的圖象有且只有一個公共點,直接寫出m的取值范圍。
②如果點A(0,t)到y=x+2的0分函數y[0]的圖象的距離小于1,直接寫出t的取值范圍。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,將一條數軸在原點O和點B處各折一下,得到一條“折線數軸”.圖中點A表示﹣11,點B表示10,點C表示18,我們稱點A和點C在數軸上相距29個長度單位.動點P從點A出發,以2單位/秒的速度沿著“折線數軸”的正方向運動,從點O運動到點B期間速度變為原來的一半,之后立刻恢復原速;同時,動點Q從點C出發,以1單位/秒的速度沿著數軸的負方向運動,從點B運動到點O期間速度變為原來的兩倍,之后也立刻恢復原速.設運動的時間為t秒.
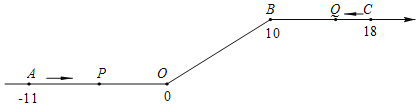
問:(1)動點P從點A運動至C點需要多少時間?
(2)P、Q兩點相遇時,求出相遇點M所對應的數是多少;
(3)求當t為何值時,P、O兩點在數軸上相距的長度與Q、B兩點在數軸上相距的長度相等.
查看答案和解析>>
科目:初中數學 來源: 題型:
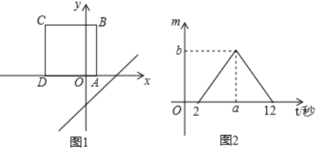
【題目】如圖1,將正方形ABCD置于平面直角坐標系中,其中AD邊在x軸上,其余各邊均與坐標軸平行,直線l:y=x﹣3沿x軸的負方向以每秒1個單位的速度平移,在平移的過程中,該直線被正方形ABCD的邊所截得的線段長為m,平移的時間為t(秒),m與t的函數圖象如圖2所示,則圖2中b的值為( )
A. 5![]() B. 4
B. 4![]() C. 3
C. 3![]() D. 2
D. 2![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】現定義運算:對于任意有理數a、b,都有a![]() b=ab-b,如:2
b=ab-b,如:2![]() 3=2×3-3,請根據以上定義解答下列各題:
3=2×3-3,請根據以上定義解答下列各題:
(1) 2![]() (-3)=___________,x
(-3)=___________,x![]() (-2)=___________;
(-2)=___________;
(2) 化簡:[(-x)![]() 3]
3] ![]() (-2);
(-2);
(3) 若x![]()
![]() =3
=3![]() (-x),求x的值.
(-x),求x的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com