【題目】如圖所示，在□ABCD中，E，F分別在BC，AD上，若想使四邊形AFCE為平行四邊形，須添加一個條件，這個條件可以是（ ）
①AF=CF；②AE=CF；③∠BAE=∠FCD；④∠BEA=∠FCE。
A. ①或② B. ②或③ C. ③或④ D. ①或③或④
暑假作業(yè)暑假快樂練西安出版社系列答案科目：初中數學 來源： 題型：
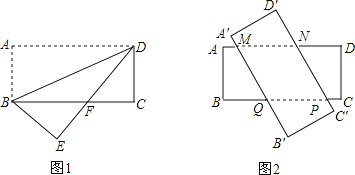
【題目】有兩張相同的矩形紙片ABCD和A′B′C′D′，其中AB=3，BC=8．
（1）若將其中一張矩形紙片ABCD沿著BD折疊，點A落在點E處（如圖1），設DE與BC相交于點F，求BF的長；
（2）若將這兩張矩形紙片交叉疊放（如圖2），判斷四邊形MNPQ的形狀，并證明．四邊形MNPQ的最大面積是_________.（直接寫出結果）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，直線y=x+2與拋物線y=ax2+bx+6（a≠0）相交于A（ 
， 
）和B（4，m），點P是線段AB上異于A、B的動點，過點P作PC⊥x軸于點D，交拋物線于點C．
（1）求拋物線的解析式；
（2）是否存在這樣的P點，使線段PC的長有最大值？若存在，求出這個最大值；若不存在，請說明理由；
（3）求△PAC為直角三角形時點P的坐標．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】閱讀下列材料：
小明在一本課外讀物上看到一道有意思的數學題：例1、解不等式：
，根據絕對值的幾何意義，到原點距離小于1的點在數軸上集中在－1和+1之間，如圖:
所以，該不等式的解集為－1<x<1．
因此，不等式
的解集為x<－1或x>1．
根據以上方法小明繼續(xù)探究：例2：求不等式：
的解集，即求到原點的距離大于2小于5的點的集合就集中在這樣的區(qū)域內，如圖：
所以，不等式的解集為－5<x<－2或2<x<5．
仿照小明的做法解決下面問題：
（1）不等式
的解集為____________．
（2）不等式
的解集是____________．
（3）求不等式
的解集．
查看答案和解析>>
科目：初中數學 來源： 題型：
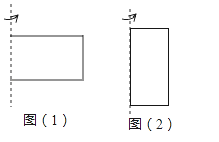
【題目】如圖，長方形的長和寬分別是7cm和3cm，分別繞著它的長和寬所在的直線旋轉一周，回答下列問題：
（1）如圖（1），繞著它的寬所在的直線旋轉一周，所得到的是什么樣的幾何體？得到的幾何體的體積是多少？（π取3.14）
（2）如圖（2），繞著它的長所在的直線旋轉一周，所得到的是什么樣的幾何體？得到的幾何體的體積是多少？（π取3.14）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，以扇形OAB的頂點O為原點，半徑OB所在的直線為x軸，建立平面直角坐標系，點B的坐標為（2，0），若拋物線y= 
x2+k與扇形OAB的邊界總有兩個公共點，則實數k的取值范圍是 ． 
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，已知Rt△ABC中，∠ACB＝90°，CA＝CB，D是AC上一點，E在BC的延長線上，且AE＝BD，BD的延長線與AE交于點F.試通過觀察、測量、猜想等方法來探索BF與AE有何特殊的位置關系，并說明你猜想的正確性．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】順次連接四邊形各邊中點，所得的圖形是__________。順次連接對角線______________的四邊形的各邊中點所得的圖形是矩形。順次連接對角線_________的四邊形的各邊中點所得的四邊形是菱形。順次連接對角線_________的四邊形的各邊中點所得的四邊形是正方形。
查看答案和解析>>
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
