
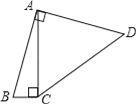
【題目】如圖,四邊形ABCD中,∠BAD=∠ACB=90°,AB=AD,AC=4BC,設(shè)CD的長為x,四邊形ABCD的面積為y,則y與x之間的函數(shù)關(guān)系式是( )
A. y=![]() B. y=
B. y=![]() C. y=
C. y=![]() D. y=
D. y=![]()
【答案】C
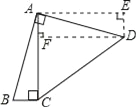
【解析】作AE⊥AC,DE⊥AE,兩線交于E點,作DF⊥AC垂足為F點,
∵∠BAD=∠CAE=90°,即∠BAC+∠CAD=∠CAD+∠DAE,∴∠BAC=∠DAE
又∵AB=AD,∠ACB=∠E=90°,
∴△ABC≌△ADE(AAS),
∴BC=DE,AC=AE,
設(shè)BC=a,則DE=a,DF=AE=AC=4BC=4a,
CF=AC﹣AF=AC﹣DE=3a,
在Rt△CDF中,由勾股定理得,
CF2+DF2=CD2,即(3a)2+(4a)2=x2,
解得:a=![]() ,
,
∴y=S四邊形ABCD=S梯形ACDE=![]() ×(DE+AC)×DF=
×(DE+AC)×DF=![]() ×(a+4a)×4a=10a2=
×(a+4a)×4a=10a2=![]() x2,
x2,
故選C.


 期末集結(jié)號系列答案
期末集結(jié)號系列答案科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在ABC中,AP=DP,DE=DF,DE⊥AB于E,DF⊥AC于F,則下列結(jié)論:①.AD平分∠BAC;②.△BED≌△FPD;③.DP∥AB;④.DF是PC的垂直平分線.其中正確的是= _________ .(寫序號)

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在△ABC中,AB =AC=2,∠B = 40°,點D在線段BC上運動(不與點B,C重合),連接AD,作∠ADE = 40°,DE交線段AC于點E.
(1)當∠BDA = 115°時,∠BAD= °,∠DEC = °,當點D從點B向點C運動時,∠BDA逐漸變 (填“大”或“小”) .
(2)當DC等于多少時,△ABD≌△DCE?請說明理由.
(3)在點D的運動過程中,是否存在△ADE是等腰三角形?若存在,請直接寫出此時∠BDA的度數(shù);若不存在,請說明理由.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】有長為1cm、2cm、3cm、4cm的四根木棒,選其中的3根作為三角形的邊,可以圍成的三角形的個數(shù)是( )
A. 1個B. 2個C. 3個D. 4個
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com