⊙O中的弦AB長等于半徑長，則弦AB所對的圓周角是 °．
【答案】
分析：首先根據題意畫出圖形，再根據“⊙O中的弦AB長等于半徑長”得到等邊三角形，則弦所對的圓心角為60度，要求這條弦所對的圓周角分兩種情況：圓周角的頂點在弦所對的劣弧或優弧上，利用圓周角定理和圓內接四邊形的性質即可求出兩種類型的圓周角．
解答：解：如圖，
AB為⊙O的弦，且AB=OA=BO，
∴△ABO為等邊三角形，
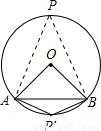
∴∠AOB=60°，
∴∠P=
∠AOB=30°，
∴∠P′=180°-∠P=180°-30°=150°．
∠P、∠P′都是弦AB所對的圓周角．
所以圓的弦長等于半徑，則這條弦所對的圓周角是30°或150°．
故答案為：30°或150°．
點評：本題主要考查了圓周角定理：在同圓和等圓中，同弧或等弧所對的圓周角相等，一條弧所對的圓周角是它所對的圓心角的一半．同時考查了一條弦所對的圓周角有兩種情形：圓周角的頂點在弦所對的劣弧或優弧上．
