
【題目】已知△ABC 中,a、b、c分別為∠A、∠B、∠C的對邊,則下列條件中:①a=4,b=7![]() ;c=8
;c=8![]() ;②a2:b2:C2=1:3:2;③∠A:∠B:∠C=3:4:5;④∠A=2∠B=2∠C.其中能判斷△ABC是直角三角形的有( )個.
;②a2:b2:C2=1:3:2;③∠A:∠B:∠C=3:4:5;④∠A=2∠B=2∠C.其中能判斷△ABC是直角三角形的有( )個.
A. 1B. 2C. 3D. 4
【答案】C
【解析】
分別根據三角形內角和定理、勾股定理的逆定理對各選項進行逐一分析即可.
①∵a2+b2=![]() =(
=(![]() )2,c2=(8
)2,c2=(8![]() )2=(
)2=(![]() )2
)2
∴a2+b2=c2,
∴此三角形是直角三角形,故本小題正確;
②∵a2:b2:c2=1:3:2,
∴設a2=x,則b2=3x,c2=2x,
∵x+2x=3x,
∴a2+c2=b2,
∴此三角形是直角三角形,故本小題正確;
③∵∠A:∠B:∠C=3:4:5,
∴設∠A=3x,則∠B=4x,∠C=5x.
∵∠A+∠B+∠C=180°,
∴3x+4x+5x=180°,
解得x=15°,
∴∠A=45°,∠B=60°,∠C=75°,
∴此三角形不是直角三角形,故本小題錯誤;
④∵∠A=2∠B=2∠C,
∴設∠B=∠C=x,則∠A=2x,
∴x+x+2x=180°,
解得:x=45°,
∴∠A=2x=90°,
∴此三角形是直角三角形,故本小題正確.
故選C.


科目:初中數學 來源: 題型:
【題目】已知數軸上三點A,O,B表示的數分別為6,0,-4,動點P從A出發,以每秒6個單位的速度沿數軸向左勻速運動.
(1)當點P到點A的距離與點P到點B的距離相等時,點P在數軸上表示的數是 ;
(2)另一動點R從B出發,以每秒4個單位的速度沿數軸向左勻速運動,若點P、R同時出發,問點P運動多少時間追上點R?
(3)若M為AP的中點,N為PB的中點,點P在運動過程中,線段MN的長度是否發生變化?若發生變化,請你說明理由;若不變,請你畫出圖形,并求出線段MN的長度.
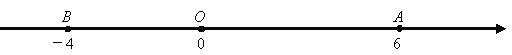
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙兩名隊員參加射擊訓練,成績分別被作成下列兩個統計圖:
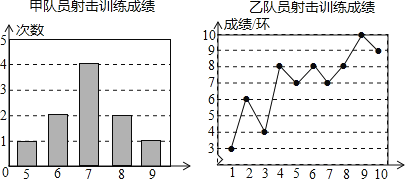
根據以上信息,整理分析數據如下:
平均成績/環 | 中位數/環 | 眾數/環 | 方差 | |
甲 | 7 | 7 | 1.2 | |
乙 | 7 | 8 |
(1)請計算甲的平均成績,乙的訓練成績的中位數和方差;(列式解答)
(2)分別運用表中的四個統計量,簡要分析這兩名隊員的射擊訓練成績.若選派其中一名參賽,你認為應選哪名隊員?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知四邊形ABCD是平行四邊形,下列結論中不正確的是( )

A. 當AB=BC時,四邊形ABCD是菱形
B. 當AC⊥BD時,四邊形ABCD是菱形
C. 當∠ABC=90°時,四邊形ABCD是矩形
D. 當AC=BD時,四邊形ABCD是正方形
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】類似于運算符號“![]() ”,新定義一種運算符號“⊙”,觀察下列運算:
”,新定義一種運算符號“⊙”,觀察下列運算:
1⊙3=1×5 +3 =8;
3⊙(-1)= 3×5+(-1)=14;
(-3)⊙4=(-3)×5+4=-11
(-5)⊙(-4)=(-5)×5+(-4)=-29 ;
(1) 歸納:用代數式表示a⊙b的結果為: ;
(2) 若2x⊙![]() =16,求
=16,求![]() 的值;
的值;
(3) 若a⊙![]() = 4,請計算
= 4,請計算![]() ⊙
⊙![]() 的值;
的值;
(4) 比較 ![]() ⊙
⊙![]() 與
與![]() ⊙(
⊙(![]() )的大小,并說理由.
)的大小,并說理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC在直角坐標系中,

(1)請寫出△ABC各點的坐標.
(2)求出△ABC的面積.
(3)若把△ABC向上平移2個單位,再向右平移2個單位得到△A′B′C′,請在圖中畫出△A′B′C′,并寫出點A′、B′、C′的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】《中華人民共和國道路交通管理條例》規定:“小汽車在城市街道上的行駛速度不得超過70km/h”,一輛小汽車在一條城市街道上由西向東行駛,在距路邊25m處有“車速檢測儀O”,測得該車從北偏西60°的A點行駛到北偏西30°的B點,所用時間為1.5s.
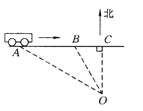
(1)試求該車從A點到B點的平均速度;
(2)試說明該車是否超過限速.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某工藝廠計劃一周生產工藝品2100個,平均每天生產300個,但實際每天生產量與計劃相比有出入.下表是某周的生產情況(超產記為正、減產記為負):

(1)寫出該廠星期一生產工藝品的數量;
(2)本周產量最多的一天比最少的一天多生產多少個工藝品?
(3)請求出該工藝廠在本周實際生產工藝品的數量;
(4)已知該廠實行每周計件工資制,每生產一個工藝品可得60元,若超額完成任務,則超過部分每個另獎50元,少生產一個扣80元.試求該工藝廠在這一周應付出的工資總額.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,有兩個可以自由轉動的均勻轉盤A、B,轉盤A被分為3等份,分別標有1、2、3三個數字;轉盤B被分為4等份,分別標有3、4、5、6四個數字;有人為甲、乙兩人設計了一個游戲規則:自由轉動轉盤A和B,轉盤停止后,指針各指向一個數字(若指針恰好停在分界線上時,當作指向右邊的數字),將指針所指的兩個數字相加,如果和為6,那么甲獲勝,否則乙獲勝。

請你用概率的有關知識進行說明,這個游戲規則是否公平?如果不公平,那么誰獲勝的可能性大些?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com