Question

【題目】如圖，已知拋物線y=-x2+bx+c與一直線相交于A（-1，0），C（2，3）兩點，與y軸交于點N．其頂點為D．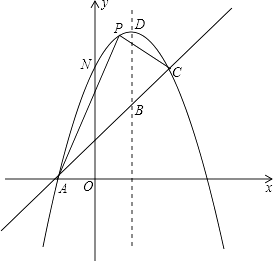

（1）拋物線及直線AC的函數關系式；
（2）設點M（3，m），求使MN+MD的值最小時m的值；
（3）若拋物線的對稱軸與直線AC相交于點B，E為直線AC上的任意一點，過點E作EF∥BD交拋物線于點F，以B，D，E，F為頂點的四邊形能否為平行四邊形？若能，求點E的坐標；若不能，請說明理由；
（4）若P是拋物線上位于直線AC上方的一個動點，求△APC的面積的最大值．

Answer 1

【答案】
（1）解：由拋物線y=-x2+bx+c過點A（-1，0）及C（2，3）得，

，

解得 ，

故拋物線為y=-x2+2x+3

又設直線為y=kx+n過點A（-1，0）及C（2，3）得

，

解得

故直線AC為y=x+1

（2）解：如圖1，作N點關于直線x=3的對稱點N′，則N′（6，3），由（1）得D（1，4），

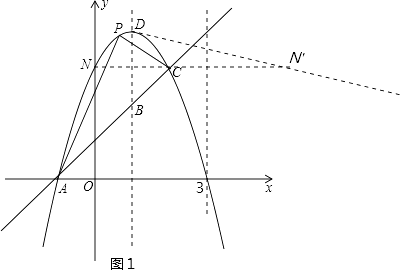
故直線DN′的函數關系式為y=- x+ ，

當M（3，m）在直線DN′上時，MN+MD的值最小，

則m=- ×3+ =

（3）解：由（1）、（2）得D（1，4），B（1，2），

∵點E在直線AC上，

設E（x，x+1），

①當點E在線段AC上時，點F在點E上方，

則F（x，x+3），

∵F在拋物線上，

∴x+3=-x2+2x+3，

解得，x=0或x=1（舍去）

∴E（0，1）；

②當點E在線段AC（或CA）延長線上時，點F在點E下方，

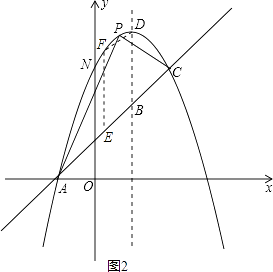
則F（x，x-1）

由F在拋物線上

∴x-1=-x2+2x+3

解得x= 或x=

∴E（ ， ）或（ ， ）

綜上，滿足條件的點E的坐標為（0，1）、（ ， ）或（ ， ）

（4）解：如圖3，過點P作PQ⊥x軸交AC于點Q，交x軸于點H；過點C作CG⊥x軸于點G，

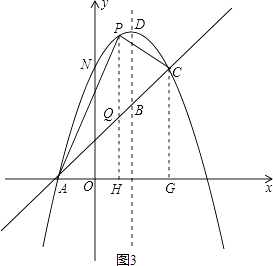
設Q（x，x+1），則P（x，-x2+2x+3）

∴PQ=（-x2+2x+3）-（x+1）

=-x2+x+2

又∵S△APC=S△APQ+S△CPQ

= PQAG

= （-x2+x+2）×3

=- （x- ）2+

∴面積的最大值為

【解析】（1）由A，C兩點的坐標，用待定系數法求出拋物線和直線AC的函數關系式；（2）由使MN+MD的值最小，得到當M（3，m）在直線DN′上時，MN+MD的值最小，求出m的值；（3）由（1）、（2）得到D，B的坐標，由點E在直線AC上，求出點E的坐標；當點E在線段AC（或CA）延長線上時，點F在點E下方，由F在拋物線上，求出點E的坐標；（4）根據題意得到PQ的代數式，由三角形的面積公式S△APC=S△APQ+S△CPQ= PQAG，求出△APC的面積的最大值；此題是綜合題，難度較大，計算和解方程時需認真仔細．