【題目】八年級（1）班張山同學利用所學函數知識，對函數
進行了如下研究：
列表如下：
x | … |
|
|
|
|
| 0 | 1 | 2 | 3 | … |
y | … | 7 | 5 | 3 | m | 1 | n | 1 | 1 | 1 | … |
描點并連線（如下圖）
（1）自變量x的取值范圍是________；
（2）表格中：
________，
________；
（3）在給出的坐標系中畫出函數的圖象；
（4）一次函數
的圖象與函數的圖象交點的坐標為_______.
【答案】（1）全體實數；（2）1，1；（3）見解析；（4）
和
.
【解析】
（1）根據函數解析式，可得答案；
（2）根據自變量與函數值得對應關系，可得答案；
（3）根據描點法畫函數圖象，可得答案；
（4）根據圖象，可得答案．
解：（1）∵函數y=|x+2|-x-1
∴自變量x的取值范圍為全體實數
故答案為：全體實數；
（2）當x=-2時，m=|-2+2|+2-1=1，
當x=0時，n=|0+2|-0-1=1，
∴
故答案為：1，1；
（3）如下圖
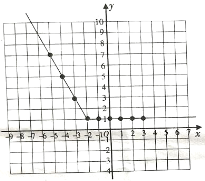
（4）在（3）中坐標系中作出直線y=-x+3，如下：
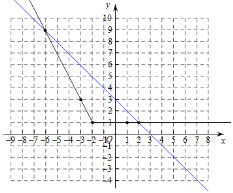
由圖象得：一次函數y=-x+3的圖象與函數y=|x+2|-x-1的圖象交點的坐標為：（-6，9）和（2，1）
故答案為：（-6，9）和（2，1）．
新思維假期作業暑假吉林大學出版社系列答案
藍天教育暑假優化學習系列答案科目：初中數學 來源： 題型：
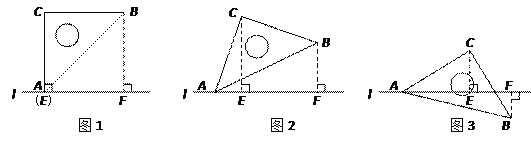
【題目】在平面內有一等腰直角三角板(∠ACB＝90)和直線l．過點C作CE⊥l于點E，過點B作BF⊥l于點F．當點E與點A重合時(圖①)，易證：AF＋BF＝2CE．當三角板繞點A順時針旋轉至圖②.圖③的位置時，上述結論是否仍然成立？若成立，請給予證明；若不成立，請直接寫出線段AF.BF.CE之間的數量關系的猜想(不需證明)．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】用小立方體搭一個幾何體，使它的主視圖和俯視圖如圖所示，俯視圖中小正方形中字母表示在該位置小立方體的個數，請解答下列問題：
（1）直接寫出a，b，c的值；
（2）這個幾何體最少有幾個小立方體搭成，最多有幾個小立方體搭成；
（3）當d＝1，e＝2，f＝1時畫出這個幾何體的左視圖．
查看答案和解析>>
科目：初中數學 來源： 題型：
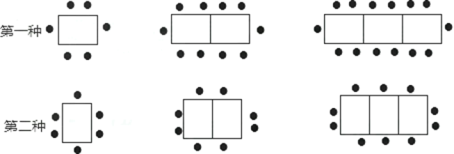
【題目】學校餐廳中，一張桌子可坐6人，現有以下兩種擺放方式:
（1）當有5張桌子時，第一種方式能坐 人，第二種方式能坐 人．
（2）當有n張桌子時，第一種方式能坐 人，第二種方式能坐 人．
（3）新學期有200人在學校就餐，但餐廳只有60張這樣的餐桌，若你是老師，你打算選擇以下哪種方式來擺放餐桌?為什么?
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在正方形ABCD中，E是AB上一點，F是AD延長線上一點，且DF＝BE.
(1)求證：CE＝CF；
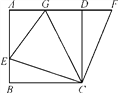
(2)若點G在AD上，且∠GCE＝45°，則GE＝BE＋GD成立嗎？為什么？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，直線
和
相交于點C，分別交x軸于點A和點B點P為射線BC上的一點。
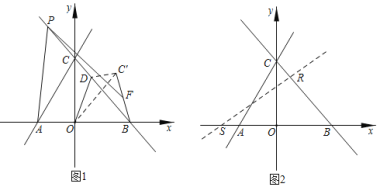
（1）如圖1，點D是直線CB上一動點，連接OD，將
沿OD翻折，點C的對應點為
，連接
，并取的中點F，連接PF，當四邊形AOCP的面積等于
時，求PF的最大值；
（2）如圖2，將直線AC繞點O順時針方向旋轉α度
，分別與x軸和直線BC相交于點S和點R，當
是等腰三角形時，直接寫出α的度數.
查看答案和解析>>
科目：初中數學 來源： 題型：
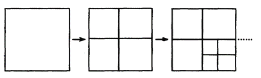
【題目】數學實踐課中：一張紙片，第一次將其撕成四小片,以后每次都將其中一片撕成更小的四片，如此進行下去,撕到第2次手中共有7張紙片，問撕到第4次時，手中共有_____張，撕到第n次時，手中共有_________________（用含有n的代數式表示）張．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在平面直角坐標系中，有若干個整數點，其順序按圖中“
”方向排列，如
，
，
，
，
，
根據這個規律探索可得，第100個點的坐標為
A.
B.
C.
D.
查看答案和解析>>
科目：初中數學 來源： 題型：
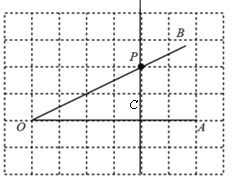
【題目】如圖，所有小正方形的邊長都為1，點O、P均在格點上，點P是∠AOB 的邊 OB 上一點，直線PC⊥OA，垂足為點C.
（1）過點 P 畫 OB 的垂線，交OA 于點D；
（2）線段 的長度是點O到直線PD 的距離；
（3）根據所畫圖形，判斷∠OPC ∠PDC（填“＞”，“＜”或“＝”），理由是 ．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
