
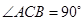 ,
,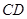 是
是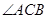 的平分線,點
的平分線,點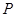 在
在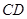 上,
上,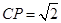 .將三角板的直角頂點放置在點
.將三角板的直角頂點放置在點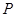 處,繞著點
處,繞著點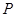 旋轉,三角板的一條直角邊與射線
旋轉,三角板的一條直角邊與射線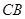 交于點
交于點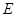 ,另一條直角邊與直線
,另一條直角邊與直線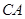 、直線分別交于點
、直線分別交于點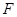 、點
、點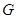 .
.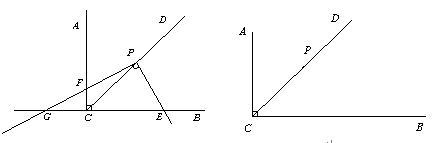
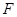 在射線
在射線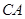 上時,
上時,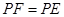 ;
;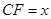 ,
,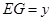 ,求
,求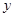 與
與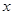 的函數解析式并寫出函數的定義域;
的函數解析式并寫出函數的定義域; 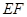 ,當△
,當△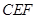 與△
與△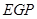 似時,求
似時,求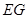 的長.
的長. (2)
(2)
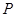 作
作 ,
, ,垂足分別為
,垂足分別為 、
、 .
. 
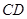 是
是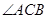 的平分線,
的平分線, .
. ,得
,得 .
. .
.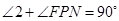 ,
, .
.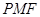 ≌△
≌△ . (3分)
. (3分)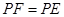 .
. 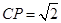 ,
, .
.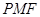 ≌△
≌△ ,
, .
. . (2分)
. (2分) ∥
∥ ,
, .
. . (2分)
. (2分) (2分)
(2分)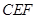 與△
與△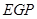 相似時,點
相似時,點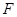 的位置有兩種情況:
的位置有兩種情況: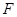 在射線
在射線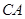 上時,
上時,
 ,
, ,
, .
. .
. .
.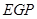 中,
中, . (2分)
. (2分)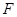 在
在 延長線上時,
延長線上時,
 ,
, ,
, .
. ,
, ,
, .
. ,可得
,可得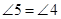 .
. .
. .
.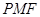 ≌△
≌△ ,
, .
. ∥
∥ ,
, .
. .
. . (2分)
. (2分)

 金牌教輔培優優選卷期末沖刺100分系列答案
金牌教輔培優優選卷期末沖刺100分系列答案科目:初中數學 來源:不詳 題型:填空題
查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題
 (千米)與所經過的時間
(千米)與所經過的時間 (分鐘)之間的函數關系,請根據圖象回答下列問題:
(分鐘)之間的函數關系,請根據圖象回答下列問題: (千米)與所經過的時間
(千米)與所經過的時間 (分鐘)之間的函數關系;
(分鐘)之間的函數關系;
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com