
【題目】如圖1,二次函數y=-x2+2x+3的圖象與x軸交于點A、B,與y軸交于點C,頂點為D.
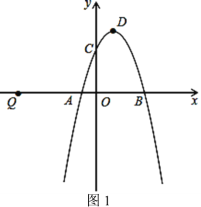
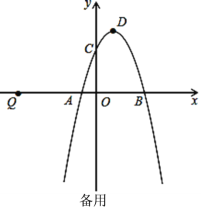
(1)寫出A、B、D三點的坐標;
(2)若P(0,t)(t<-1)是y軸上一點,Q(-5,0),將點Q繞著點P順時針方向旋轉90°得到點E.當點E恰好在該二次函數的圖象上時,求t的值;
(3)在(2)的條件下,連接AD、AE.若M是該二次函數圖象上一點,且∠DAE=∠MCB,求點M的坐標.
【答案】(1)A(-1,0),B(3,0),D(1,4);(2)所求t的值為-2;(3)M(![]() ,
,![]() )或M(4,-5).
)或M(4,-5).
【解析】
(1)y=-x2+2x+3,令x=0,則y=3,令y=0,則x=3或-1,即可求解;
(2)△EPH≌△PQO(AAS),則EH=OP=-t,HP=OQ=5,E(-t,5+t),當點E恰好在該二次函數的圖象上時,有5+t=-t2-2t+3,即可求解;
(3)分點M在x軸上、點M在x軸兩種情況,分別求解即可.
(1)y=-x2+2x+3,令x=0,則y=3,令y=0,則x=3或-1,
故:A(-1,0),B(3,0),D(1,4);
(2)如圖1,過點E作EH⊥y軸于點H,
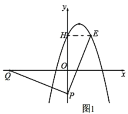
∵∠PQO+∠OPQ=90°,
∠OPQ+∠HPE=90°,
∴∠HPE=∠PQO,
由旋轉知,PQ=PE,
∴△EPH≌△PQO(AAS),
∴EH=OP=-t,
HP=OQ=5
∴E(-t,5+t)
當點E恰好在該二次函數的圖象上時,
有5+t=-t2-2t+3
解得t1=-2,t2=-1(由于t<-1所以舍去),
故所求t的值為-2;
(3)設點M(a,-a2+2a+3)
①若點M在x軸上方,
如圖2,過點M作MN⊥y軸于點N,過點D作DF⊥x軸于點F.
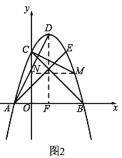
∵∠EAB=∠OCB=45°,
∠DAE=∠MCB
∴∠MCN=∠DAF
∴△MCN∽△DAF,
∴![]() ,
,
∴![]() ,a2=0(舍去),
,a2=0(舍去),
∴M(![]() ,
,![]() ) ;
) ;
②若點M在x軸下方,

用同樣的方法得M(4,-5),
綜上所述,M(![]() ,
,![]() )或M(4,-5).
)或M(4,-5).


 開心快樂假期作業暑假作業西安出版社系列答案
開心快樂假期作業暑假作業西安出版社系列答案 名題訓練系列答案
名題訓練系列答案 期末集結號系列答案
期末集結號系列答案科目:初中數學 來源: 題型:
【題目】甲乙兩人輪流在黑板上寫下不超過 ![]() 的正整數(每次只能寫一個數),規定禁止在黑板上寫已經寫過的數的約數,最后不能寫的為失敗者,如果甲寫第一個,那么,甲寫數字( )時有必勝的策略.
的正整數(每次只能寫一個數),規定禁止在黑板上寫已經寫過的數的約數,最后不能寫的為失敗者,如果甲寫第一個,那么,甲寫數字( )時有必勝的策略.
A. 10 B. 9 C. 8D.6
查看答案和解析>>
科目:初中數學 來源: 題型:
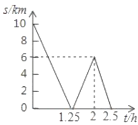
【題目】一條公路旁依次有![]() ,
,![]() ,
,![]() 三個村莊,甲乙兩人騎自行車分別從
三個村莊,甲乙兩人騎自行車分別從![]() 村、
村、![]() 村同時出發前往
村同時出發前往![]() 村,甲乙之間的距離
村,甲乙之間的距離![]() 與騎行時間
與騎行時間![]() 之間的函數關系如圖所示,下列結論:
之間的函數關系如圖所示,下列結論:
①![]() ,
,![]() 兩村相距
兩村相距![]() ; ②出發
; ②出發![]() 后兩人相遇;
后兩人相遇;
③甲每小時比乙多騎行![]() ; ④相遇后,乙又騎行了
; ④相遇后,乙又騎行了![]() 時兩人相距
時兩人相距![]() .
.
其中正確的有_____________________.(填序號)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,O為原點,點A(2,0),點P(1,m)(m>0)和點Q關于x軸對稱.過點P作PB∥x軸,與直線AQ交于點B,如果AP⊥BO,求點P的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,是由一些棱長為單位1的相同的小正方體組合成的簡單幾何體.
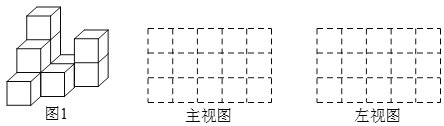
(1)圖中有 個小正方體;
(2)請在圖1右側方格中分別畫出幾何體的主視圖、左視圖;
(3)不改變(2)中所畫的主視圖和左視圖,最多還能在圖1中添加 個小正方體.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一個不透明的口袋中裝有4個完全相同的小球,分別標有數字1,2,3,4,另外有一個可以自由旋轉的圓盤,被分成面積相等的3個扇形區域,分別標有數字1,2,3(如圖所示).

(1)從口袋中摸出一個小球,所摸球上的數字大于2的概率為 ;
(2)小龍和小東想通過游戲來決定誰代表學校參加歌詠比賽,游戲規則為:一人從口袋中摸出一個小球,另一人轉動圓盤,如果所摸球上的數字與圓盤上轉出數字之和小于5,那么小龍去;否則小東去.你認為游戲公平嗎?請用樹狀圖或列表法說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,正方形網格中,每個小正方形的邊長都是一個單位長度,在平面直角坐標系中,△OAB的三個頂點O(0,0)、A(4,1)、B(4,4)均在格點上.
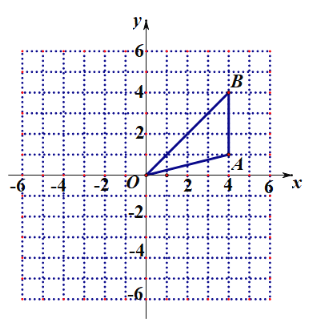
(1)畫出△OAB繞原點![]() 順時針旋轉
順時針旋轉![]() 后得到的△
后得到的△![]() ,并寫出點
,并寫出點![]() 的坐標;
的坐標;
(2)在(1)的條件下,求線段![]() 在旋轉過程中掃過的扇形的面積.
在旋轉過程中掃過的扇形的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,在平面直角坐標系中,拋物線![]() 經過點
經過點![]() 和點
和點![]() .
.
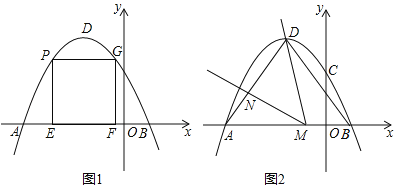
(1)求拋物線的解析式及頂點![]() 的坐標;
的坐標;
(2)點![]() 是拋物線上
是拋物線上![]() 、
、![]() 之間的一點,過點
之間的一點,過點![]() 作
作![]() 軸于點
軸于點![]() ,
,![]() 軸,交拋物線于點
軸,交拋物線于點![]() ,過點
,過點![]() 作
作![]() 軸于點
軸于點![]() ,當矩形
,當矩形![]() 的周長最大時,求點
的周長最大時,求點![]() 的橫坐標;
的橫坐標;
(3)如圖2,連接![]() 、
、![]() ,點
,點![]() 在線段
在線段![]() 上(不與
上(不與![]() 、
、![]() 重合),作
重合),作![]() ,
,![]() 交線段
交線段![]() 于點
于點![]() ,是否存在這樣點
,是否存在這樣點![]() ,使得
,使得![]() 為等腰三角形?若存在,求出
為等腰三角形?若存在,求出![]() 的長;若不存在,請說明理由.
的長;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】廬陽春風體育運動品商店從廠家購進甲,乙兩種T恤共400件,其每件的售價與進貨量m(件)之間的關系及成本如下表所示:
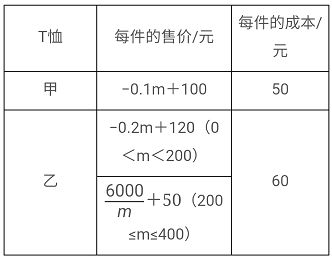
(1)當甲種T恤進貨250件時,求兩種T恤全部售完的利潤是多少元.
(2)若所有的T恤都能售完,求該店獲得的總利潤y(元)與乙種T恤的進貨量x(件)之間的函數關系式;
(3)在(2)的條件下已知兩種T恤進貨量都不低于100件,且所進的T恤全部售完,該商店如何安排進貨才能獲得的利潤最大?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com