【題目】如圖，已知： 
平分
， 
垂直平分
， 
， 
，垂足分別是點
、
．求證(1) 
；(2) 
．
【答案】（1）證明見解析；（2）證明見解析.
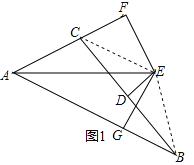
【解析】試題分析：（1）連接CE、BE，根據線段垂直平分線的性質得到EC=EB，根據角平分線的性質得到EF=EG，于是證得Rt△CFE≌Rt△BGE，即可得到結論；
（2）根據AE平分∠BAC，EF⊥AC，EG⊥AB，得到EF=EG，證得Rt△AGE≌Rt△AFE，得到AG=AF，于是得到結論．
試題解析：證明：（1）連接CE、BE，∵ED垂直平分BC，∴EC=EB，∵AE平分∠CAB，EF⊥AC，EG⊥AB，∴EF=EG，在Rt△CFE和Rt△BGE中，∵EC=EB，EF=EG，∴Rt△CFE≌Rt△BGE，∴BG=CF；
（2）∵AE平分∠BAC，EF⊥AC，EG⊥AB，∴EF=EG，在Rt△AGE和Rt△AFE中，∵AE=AE，EG=EF，∴Rt△AGE≌Rt△AFE，∴AG=AF，∵AB=AG+BG，∴AB=AF+CF．
手拉手全優練考卷系列答案科目：初中數學 來源： 題型：
【題目】（12分）某公交公司有A，B型兩種客車，它們的載客量和租金如下表：
紅星中學根據實際情況，計劃租用A，B型客車共5輛，同時送七年級師生到基地校參加社會實踐活動，設租用A型客車x輛，根據要求回答下列問題：
（1）用含x的式子填寫下表：
（2）若要保證租車費用不超過1900元，求x的最大值；
（3）在（2）的條件下，若七年級師生共有195人，寫出所有可能的租車方案，并確定最省錢的租車方案．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】計算：
(1)－23＋
(2018＋3)0－
； (2)992－69×71；
(3) 
÷(－3xy)； (4)(－2＋x)(－2－x)；
(5)(a＋b－c)(a－b＋c); (6)(3x－2y＋1)2.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】閱讀材料：
關于
，
的二元一次方程
有一組整數解
則方程的全部整數解可表示為
（
為整數）.
問題：求方程
的所有正整數解.
小明參考閱讀材料，解決該問題如下：
解：該方程一組整數解為
則全部整數解可表示為
（為整數）.
因為
解得
.因為為整數，所以
0或
.
所以該方程的正整數解為
和
.
請你參考小明的解題方法， 完成下面的問題：
（1）方程
的全部正整數解為______________；
（2）方程
的全部整數解表示為： 
（為整數）；
（3）方程
的正整數解有多少組? 請說明理由.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知，點
是線段
所在平面內任意一點，分別以
、
為邊，在
同側作等邊
和等邊
，聯結
、
交于點
．
(1)如圖1，當點
在線段
上移動時，線段
與
的數量關系是:________；
(2)如圖2，當點
在直線
外，且
，仍分別以
、
為邊，在
同側作等邊
和等邊
，聯結
、
交于點
．(1)的結論是否還存在？若成立，請證明；若不成立，請說明理由．此時
是否隨
的大小發生變化？若變化，寫出變化規律，若不變，請求出
的度數；
(3)如圖3，在(2)的條件下，聯結
，求證： 
平分
．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，已知點D、F、E、G都在△ABC的邊上，EF∥AD，∠1=∠2，∠BAC=70°，求∠AGD的度數．（請在下面的空格處填寫理由或數學式）
解：∵EF∥AD，（已知）
∴∠2= （ ）
∵∠1=∠2，（已知）
∴∠1= （ ）
∴ ∥ ，（ ）
∴∠AGD+ =180°，（兩直線平行，同旁內角互補）
∵ ，（已知）
∴∠AGD= （等式性質）
查看答案和解析>>
科目：初中數學 來源： 題型：
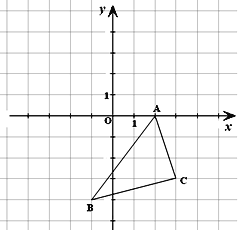
【題目】如圖所示的直角坐標系中，解答下列問題：
（1）分別寫出A、B兩點的坐標；
（2）將△ABC向左平移3個單位長度，再向上平移5個單位長度，畫出平移后的△A1B1C1；
（3）求 △A1B1C1的面積。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
