日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

精英家教網 > 初中數學 > 題目詳情
如果等邊三角形的邊長為6，那么它的內切圓的半徑為    ．
【答案】分析：首先根據題意畫出等邊三角形ABC與內切圓O．首先根據三角形面積計算公式求出S△ABC，再觀察發現三角形ABC的內切圓半徑，恰好是三角形ABC內三個三角形的高，因而可以通過面積S△ABC=S△AOB+S△BOC+S△AOC來計算．
解答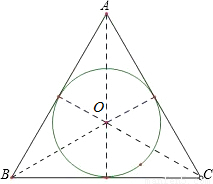：解：等邊三角形ABC的邊長為6，則該S△ABC==
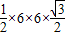
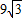
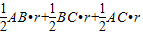
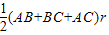
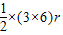
S△ABC=S△AOB+S△BOC+S△AOC====9r
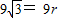
∴，即r=
故答案為
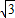點評：本題考查三角形的內切圓與內心．解決本題的關鍵是將求△ABC轉化為求S△AOB、S△BOC、S△AOC．
練習冊系列答案
相關習題

科目：初中數學 來源： 題型：

如果等邊三角形的邊長為6，那么它的外接圓的半徑為（　　）
A、2
3
B、4
C、5
D、6

查看答案和解析>>

科目：初中數學 來源： 題型：

（2002•西藏）如果等邊三角形的邊長是3cm，那么它的一條高長為
3
3
2
3
3
2
．

查看答案和解析>>

科目：初中數學 來源： 題型：

（2013•西寧）如果等邊三角形的邊長為4，那么等邊三角形的中位線長為（　　）

查看答案和解析>>

科目：初中數學 來源： 題型：

如果等邊三角形的邊長為3，那么連接各邊中點所成的三角形的周長為
9
2
9
2
．

查看答案和解析>>

科目：初中數學 來源： 題型：

如果等邊三角形的邊長為4，那么連接各邊中點所成的三角形的周長為（　　）

查看答案和解析>>

同步練習冊答案
主站蜘蛛池模板： 日本在线免费 | 亚洲蜜臀av乱码久久精品蜜桃 | 亚洲成av人片在线观看 | 久久久a | 精品伦理一区二区三区 | 一级免费黄视频 | 国产一级免费网站 | av不卡在线看 | 亚洲国产一区视频 | 国产精品综合 | 国产精品精品视频一区二区三区 | 精品1区2区 | 欧美高清不卡 | 欧美日韩成人精品 | 日韩欧美一区二区视频 | 欧美日韩电影一区二区三区 | 亚洲一区二区三区四区五区午夜 | 欧美精品h | 国产日韩91| 精品日韩欧美一区二区三区在线播放 | 欧美啪| 一区二区三区不卡视频 | 欧美成人一区二区三区片免费 | av资源首页 | www.日韩| 国产91亚洲精品 | 国产蜜臀97一区二区三区 | 国产永久免费 | 伊人av超碰久久久麻豆 | 久久电影国产免费久久电影 | 国产一区二区三区精品久久久 | 亚洲精品视频在线播放 | 热久久久 | 国产一区 | 在线观看污片 | 日韩av在线一区二区三区 | 久久久www成人免费无遮挡大片 | 国产精品一级在线 | 久久无码精品一区二区三区 | 国产视频一区在线 | 免费不卡视频 |