
【題目】知識背景:我們在第十一章《三角形》中學習了三角形的邊與角的性質,在第十二章《全等三角形》中學習了全等三角形的性質和判定,在第十三章《軸對稱》中學習了等腰三角形的性質和判定.在一些探究題中經常用以上知識轉化角和邊,進而解決問題.
問題:如圖1,![]() 是等腰三角形,
是等腰三角形,![]() ,
,![]() 是
是![]() 的中點,以
的中點,以![]() 為腰作等腰
為腰作等腰![]() ,且滿足
,且滿足![]() ,連接
,連接![]() 并延長交
并延長交![]() 的延長線于點
的延長線于點![]() ,試探究
,試探究![]() 與
與![]() 之間的數量關系.
之間的數量關系.
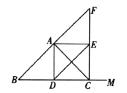
圖1
發現:(1)![]() 與
與![]() 之間的數量關系為 .
之間的數量關系為 .
探究:(2)如圖2,當點![]() 是線段
是線段![]() 上任意一點(除
上任意一點(除![]() 、
、![]() 外)時,其他條件不變,試猜想
外)時,其他條件不變,試猜想![]() 與
與![]() 之間的數量關系,并證明你的結論.
之間的數量關系,并證明你的結論.
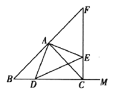
圖2
拓展:(3)當點![]() 在線段
在線段![]() 的延長線上時,在備用圖中補全圖形,并直接寫出
的延長線上時,在備用圖中補全圖形,并直接寫出![]() 的形狀.
的形狀.

備用圖
【答案】(1)![]() ;(2)
;(2)![]() ,證明見解析;(3)畫圖見解析,等腰直角三角形.
,證明見解析;(3)畫圖見解析,等腰直角三角形.
【解析】
(1)根據等腰三角形的性質即可得![]() ;
;
(2)由等腰直角三角形的性質可得![]() ,再根據全等三角形的性質及等角對等邊即可證明;
,再根據全等三角形的性質及等角對等邊即可證明;
(3)作出圖形,根據等腰三角形性質易證![]() ,進而根據角度的代換,得出結論.
,進而根據角度的代換,得出結論.
解:(1)![]() .
.
∵△ABC是等腰三角形,且![]() ,
,
![]() ,
,![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
![]() 是以
是以![]() 為腰的等腰三角形,
為腰的等腰三角形,
![]() .
.
在![]() 與
與![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
(2)![]() .
.
證明:![]() 是等腰三角形,且
是等腰三角形,且![]() ,
,
![]() ,
,![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
![]() 是以
是以![]() 為腰的等腰三角形,
為腰的等腰三角形,
![]() .
.
在![]() 與
與![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
(3)![]() 是等腰直角三角形.
是等腰直角三角形.
提示:如圖,
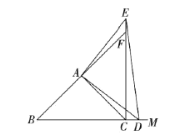
![]() 是等腰三角形,
是等腰三角形,![]() ,
,
![]() ,
,![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
![]() 是以
是以![]() 為腰的等腰三角形,
為腰的等腰三角形,
![]() .
.
在![]() 與
與![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 是等腰三角形,
是等腰三角形,
![]() ,
,
![]() 是等腰直角三角形.
是等腰直角三角形.


科目:初中數學 來源: 題型:
【題目】甲乙兩位同學用圍棋子做游戲.如圖所示,現輪到黑棋下子,黑棋下一子后白棋再下一子,使黑棋的5個棋子組成軸對稱圖形,白棋的5個棋子也成軸對稱圖形.則下列下子方法不正確的是【 】.[說明:棋子的位置用數對表示,如A點在(6,3)]

A.黑(3,7);白(5,3) B.黑(4,7);白(6,2)
C.黑(2,7);白(5,3) D.黑(3,7);白(2,6)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】數和形是數學的兩個主要研究對象,我們經常運用數形結合、數形轉化的方法解決一些數學問題.下面我們來探究“由數思形,以形助數”的方法在解決代數問題中的應用.
(1)探究![]() 的幾何意義:如圖①,在直角坐標系中,設點M的坐標為(x,y),過M作MP⊥x軸于P,作MQ⊥y軸于Q,則P點坐標為(x,0),Q點坐標為(0,y),即OP=|x|,OQ=|y|,在△OPM中,PM=OQ=|y|,則MO=
的幾何意義:如圖①,在直角坐標系中,設點M的坐標為(x,y),過M作MP⊥x軸于P,作MQ⊥y軸于Q,則P點坐標為(x,0),Q點坐標為(0,y),即OP=|x|,OQ=|y|,在△OPM中,PM=OQ=|y|,則MO=![]() ,因此,
,因此,![]() 的幾何意義可以理解為點M(x,y)與點O(0,0)之間的距離OM.
的幾何意義可以理解為點M(x,y)與點O(0,0)之間的距離OM.
①![]() 的幾何意義可以理解為點N1 (填寫坐標)與點O(0,0)之間的距離N1O;
的幾何意義可以理解為點N1 (填寫坐標)與點O(0,0)之間的距離N1O;
②點N2(5,﹣1)與點O(0,0)之間的距離ON2為 .
(2)探究![]() 的幾何意義:如圖②,在直角坐標系中,設點A′的坐標為(x﹣1,y﹣5),由探究(1)可知,A′O=
的幾何意義:如圖②,在直角坐標系中,設點A′的坐標為(x﹣1,y﹣5),由探究(1)可知,A′O=![]() ,將線段A′O先向右平移1個單位,再向上平移5個單位,得到線段AB,此時點A的坐標為(x,y),點B的坐標為(1,5),因為AB=A′O,所以AB=
,將線段A′O先向右平移1個單位,再向上平移5個單位,得到線段AB,此時點A的坐標為(x,y),點B的坐標為(1,5),因為AB=A′O,所以AB=![]() ,因此
,因此![]() 的幾何意義可以理解為點A(x,y)與點B(1,5)之間的距離.
的幾何意義可以理解為點A(x,y)與點B(1,5)之間的距離.
(3)探究![]() 的幾何意義:請仿照探究二(2)的方法,在圖③中畫出圖形,那么
的幾何意義:請仿照探究二(2)的方法,在圖③中畫出圖形,那么![]() 的幾何意義可以理解為點C (填寫坐標)與點D(x,y)之間的距離.
的幾何意義可以理解為點C (填寫坐標)與點D(x,y)之間的距離.
(4)拓展應用:①![]()
![]() 的幾何意義可以理解為:點A(x,y)與點E(1,﹣4)的距離與點A(x,y)與點F (填寫坐標)的距離之和.
的幾何意義可以理解為:點A(x,y)與點E(1,﹣4)的距離與點A(x,y)與點F (填寫坐標)的距離之和.
②![]() 的最小值為 (直接寫出結果)
的最小值為 (直接寫出結果)
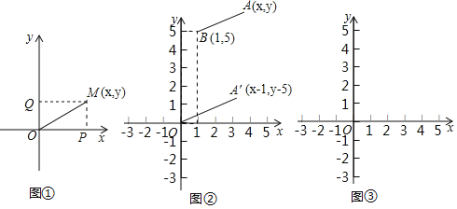
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,已知![]() 是等邊三角形,點
是等邊三角形,點![]() 的坐標是
的坐標是![]() ,點
,點![]() 在第一象限,
在第一象限,![]() 的平分線交
的平分線交![]() 軸于點
軸于點![]() ,把
,把![]() 繞著點
繞著點![]() 按逆時針方向旋轉,使邊
按逆時針方向旋轉,使邊![]() 與
與![]() 重合,得到
重合,得到![]() ,連接
,連接![]() .求:
.求:![]() 的長及點
的長及點![]() 的坐標.
的坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】六一期間,某公園游戲場舉行“迎奧運”活動.有一種游戲的規則是:在一個裝有![]() 個紅球和若干個白球(每個球除顏色外其他相同)的袋中,隨機摸一個球,摸到一個紅球就得到一個奧運福娃玩具.已知參加這種游戲活動為
個紅球和若干個白球(每個球除顏色外其他相同)的袋中,隨機摸一個球,摸到一個紅球就得到一個奧運福娃玩具.已知參加這種游戲活動為![]() 人次,公園游戲場發放的福娃玩具為
人次,公園游戲場發放的福娃玩具為![]() 個.
個.
![]() 求參加一次這種游戲活動得到福娃玩具的概率;
求參加一次這種游戲活動得到福娃玩具的概率;
![]() 請你估計袋中白球接近多少個?
請你估計袋中白球接近多少個?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】科技創新加速中國高鐵技術發展,某建筑集團承擔一座高架橋的鋪設任務,在合同期內高效完成了任務,這是記者與該集團工程師的一段對話:
記者:你們是用9天完成4800米長的高架橋鋪設任務的?
工程師:是的,我們鋪設600米后,采用新的鋪設技術,這樣每天鋪設長度是原來的2倍.
通過這段對話,請你求出該建筑集團原來每天鋪設高架橋的長度.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com