
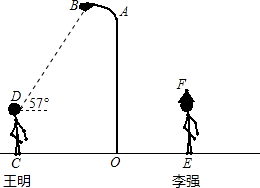
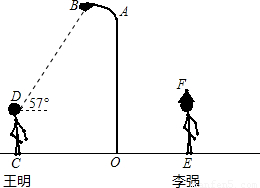
 如圖所示,點B表示籃球場的一盞照明燈.若王明到燈柱OA的距離CO為4.6米,照明燈B到燈柱OA的距離為1.6米,王明目測照明燈B的仰角為57°,他的目高DC為1.6米.
如圖所示,點B表示籃球場的一盞照明燈.若王明到燈柱OA的距離CO為4.6米,照明燈B到燈柱OA的距離為1.6米,王明目測照明燈B的仰角為57°,他的目高DC為1.6米.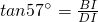 ,
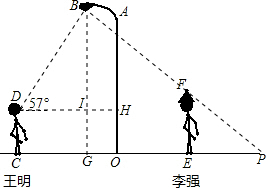
,
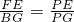 ,
,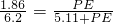 ,
,

科目:初中數學 來源: 題型:
查看答案和解析>>
科目:初中數學 來源: 題型:
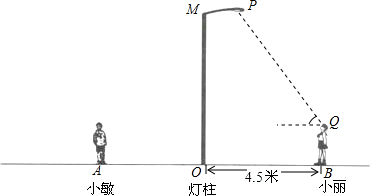
 (2013•金平區模擬)如圖所示,點B表示籃球場的一盞照明燈.若王明到燈柱OA的距離CO為4.6米,照明燈B到燈柱OA的距離為1.6米,王明目測照明燈B的仰角為57°,他的目高DC為1.6米.
(2013•金平區模擬)如圖所示,點B表示籃球場的一盞照明燈.若王明到燈柱OA的距離CO為4.6米,照明燈B到燈柱OA的距離為1.6米,王明目測照明燈B的仰角為57°,他的目高DC為1.6米.查看答案和解析>>
科目:初中數學 來源:2013年廣東省汕頭市金平區中考數學模擬試卷(解析版) 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com