
【題目】已知二次函數![]() 的圖像如圖所示.
的圖像如圖所示.
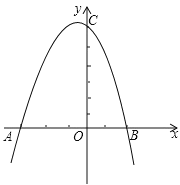
(1)當![]() 時,說明這個二次函數的圖像與x軸必有兩個交點;
時,說明這個二次函數的圖像與x軸必有兩個交點;
(2)如圖情況下,若![]() ,求點C的坐標.
,求點C的坐標.
【答案】(1)證明見詳解
(2)C的坐標是(0,6)
【解析】
(1)根據求得△值,再根據△>0來判斷二次函數的圖象與x軸必有兩個交點;
(2)將求二次函數y=-x2+(m-2)x+3(m+1)與x軸的交點轉化為求方程-x2+(m-2)x+3(m+1)=0的解,再根據一元二次方程根與系數的關系,可求得m的值,再將m的值代入二次函數.由圖中不難發現C點是二次函數與x軸的交點,令x=0,求得y的值.至此C點坐標確定.
解:(1)∵△=(m-2)2-4(-1)3(m+1)=(m+4)2
∵![]()
∴△=(m+4)2>0,
∴拋物線與x軸必有兩個交點;
(2)設方程![]() 的兩根為x1、x2,且x1<0,x2>0
的兩根為x1、x2,且x1<0,x2>0
由圖可知![]() ,由
,由![]() ,可知
,可知![]()
根據根與系數的關系,可知![]() ,
,
則m=1,于是二次函數的解析式為![]() ,
,
把x=0代入![]() ,得y=6,
,得y=6,
所以C的坐標是(0,6).


 巧學巧練系列答案
巧學巧練系列答案科目:初中數學 來源: 題型:
【題目】如圖,點 ![]() 是以
是以 ![]() 為直徑的
為直徑的 ![]() 上一點,
上一點,![]() 于點
于點 ![]() ,過點
,過點 ![]() 作
作 ![]() 的切線,與
的切線,與 ![]() 的延長線相交于點
的延長線相交于點 ![]() ,
,![]() 是
是 ![]() 的中點,連接
的中點,連接 ![]() 并延長與
并延長與 ![]() 相交于點
相交于點 ![]() ,延長
,延長 ![]() 與
與 ![]() 的延長線相交于點
的延長線相交于點 ![]() ,且
,且 ![]() .
.
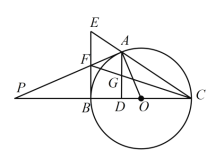
(1)求證:BF=EF;
(2)求![]() ;
;
(3)求![]() 的半徑r.
的半徑r.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】對于給定的兩個函數,任取自變量x的一個值,當x<1時,它們對應的函數值互為相反數:當x≥1時,它們對應的函數值相等,我們稱這樣的兩個函數互為相關函數,例如:一次函數y=x﹣4,它的相關函數為![]()
(1)一次函數y=﹣x+5的相關函數為 .
(2)已知點A(b﹣1,4),點B坐標(b+3,4),函數y=3x﹣2的相關函數與線段AB有且只有一個交點,求b的取值范圍;
(3)當b+1≤x≤b+2時,函數y=﹣3x+b2的相關函數的最小值為﹣3,求b的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
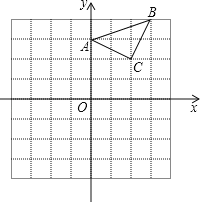
【題目】已知:△ABC在直角坐標平面內,三個頂點的坐標分別為A(0,3)、B(3,4)、C(2,2)(正方形網格中每個小正方形的邊長是一個單位長度).
(1)畫出△ABC向下平移4個單位長度得到的△A1B1C1,點C1的坐標是 ;
(2)以點B為位似中心,在網格內畫出△A2B2C2,使△A2B2C2與△ABC位似,且位似比為2:1,點C2的坐標是 ;
(3)△A2B2C2的面積是 平方單位.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】直線![]() 與x軸、y軸分別交于點A、B,拋物線
與x軸、y軸分別交于點A、B,拋物線![]() 經過點A,將點B向右平移5個單位長度,得到點C,若拋物線與線段BC恰有一個公共點,則
經過點A,將點B向右平移5個單位長度,得到點C,若拋物線與線段BC恰有一個公共點,則![]() 的取值范圍是____.
的取值范圍是____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】四邊形ABCD中,AB=BC,∠B=∠C=90°,P是BC邊上一點,AP⊥PD,E是AB邊上一點,∠BPE=∠BAP.
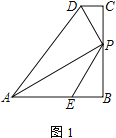
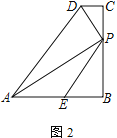
(1) 如圖1,若AE=PE,直接寫出![]() =______;
=______;
(2) 如圖2,求證:AP=PD+PE;
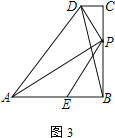
(3) 如圖3,當AE=BP時,連BD,則![]() =______,并說明理由.
=______,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】李明準備進行如下操作實驗,把一根長40 cm的鐵絲剪成兩段,并把每段首尾相連各圍成一個正方形.
(1)要使這兩個正方形的面積之和等于58 cm2,李明應該怎么剪這根鐵絲?
(2)李明認為這兩個正方形的面積之和不可能等于48 cm2,你認為他的說法正確嗎?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖是由邊長為1的小正方形構成的網格,每個小正方形的頂點叫做格點.四邊形ABCD的頂點在格點上,點E是邊DC與網格線的交點.請選擇適當的格點,用無刻度的直尺在網格中完成下列畫圖,保留連線的痕跡,不要求說明理由.
(1)如圖1,過點A畫線段AF,使AF∥DC,且AF=DC.
(2)如圖1,在邊AB上畫一點G,使∠AGD=∠BGC.
(3)如圖2,過點E畫線段EM,使EM∥AB,且EM=AB.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在國家政策的調控下,某市的商品房成交均價由今年5月份的每平方米10000元下降到7月份的每平方米8100元.
(1)求6、7兩月平均每月降價的百分率;
(2)如果房價繼續回落,按此降價的百分率,請你預測到9月份該市的商品房成交均價是否會跌破每平方米6500元?請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com