
 為O),現有射線CP繞點C從CA的位置開始按順時針方向以每秒2度的速度旋轉到CB位置,在旋轉過程中,射線CP與量角器的半圓弧交于E.
為O),現有射線CP繞點C從CA的位置開始按順時針方向以每秒2度的速度旋轉到CB位置,在旋轉過程中,射線CP與量角器的半圓弧交于E. (1)證明:連接BE,如圖所示:
(1)證明:連接BE,如圖所示: (2)解:①當射線CP經過△ABC的外心時,CP經過AB的中心且此時有:CO=AO;
(2)解:①當射線CP經過△ABC的外心時,CP經過AB的中心且此時有:CO=AO; °=45°,圓心角為90°,
°=45°,圓心角為90°,

 靈星計算小達人系列答案
靈星計算小達人系列答案科目:初中數學 來源: 題型:
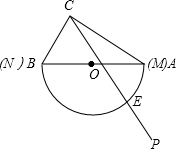 為O),現有射線CP繞點C從CA的位置開始按順時針方向以每秒2度的速度旋轉到CB位置,在旋轉過程中,射線CP與量角器的半圓弧交于E.
為O),現有射線CP繞點C從CA的位置開始按順時針方向以每秒2度的速度旋轉到CB位置,在旋轉過程中,射線CP與量角器的半圓弧交于E.查看答案和解析>>
科目:初中數學 來源:2009-2010學年江蘇省鹽城市鹽城中學九年級(上)期中數學試卷(解析版) 題型:解答題

查看答案和解析>>
科目:初中數學 來源:2009-2010學年江蘇省鹽城市初級中學九年級(上)期中數學試卷(解析版) 題型:解答題

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com