D
分析:本題可以利用銳角三角函數的定義求解,也可以利用互為余角的三角函數關系式求解.
解答:解法1:利用三角函數的定義及勾股定理求解.
∵在Rt△ABC中,∠C=90°,tanA=3,
設a=3x,b=x,則c=

x,
∴cosB=

=

.
故選D.
解法2:利用同角、互為余角的三角函數關系式求解.
又∵tanA=

=3,
∴sinA=3cosA.
又sin
2A+cos
2A=1,
∴cosA=

.
∵A、B互為余角,
∴cosB=sin(90°-B)=sinA=

.
故選D.
點評:求銳角的三角函數值的方法:利用銳角三角函數的定義,通過設參數的方法求三角函數值,或者利用同角(或余角)的三角函數關系式求三角函數值.

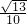



 x,
x, =
= .
. =3,
=3, .
. .
.
