
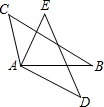
 如圖,在△CAB和△EAD中,∠CAE=∠BAD,BC=DE.
如圖,在△CAB和△EAD中,∠CAE=∠BAD,BC=DE. ,BC=2x-y+7,AC=(y-6)2,AD=
,BC=2x-y+7,AC=(y-6)2,AD=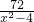 ,DE=
,DE=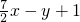 ,AE=4,請解決以下問題:
,AE=4,請解決以下問題: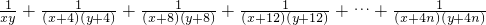 .
. =
=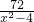 ,
,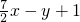 解得x=4;
解得x=4; ,
, [
[ +
+ +
+ +…+
+…+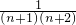 ]
] (1-
(1- +
+ -
- +
+ -
- +…+
+…+ -
- )
) (1-
(1- )=
)=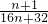 .
. =
=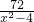 ,然后解出x的值,利用此方法依次求出BC=DE或AC=AE,從而解出x的值,再由三角形三邊關系判斷是否合題意,最后得出正確答案,x=4,y=8.②把x、y的值代入方程,然后展開化簡即可.
,然后解出x的值,利用此方法依次求出BC=DE或AC=AE,從而解出x的值,再由三角形三邊關系判斷是否合題意,最后得出正確答案,x=4,y=8.②把x、y的值代入方程,然后展開化簡即可.

科目:初中數學 來源: 題型:
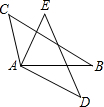 如圖,在△CAB和△EAD中,∠CAE=∠BAD,BC=DE.
如圖,在△CAB和△EAD中,∠CAE=∠BAD,BC=DE.| 12 |
| x-2 |
| 72 |
| x2-4 |
| 7 |
| 2 |
| 1 |
| xy |
| 1 |
| (x+4)(y+4) |
| 1 |
| (x+8)(y+8) |
| 1 |
| (x+12)(y+12) |
| 1 |
| (x+4n)(y+4n) |
查看答案和解析>>
科目:初中數學 來源: 題型:
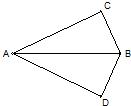 5、如圖,在△ABC和△ABD中,∠C=∠D=90°,若利用“AAS”證明△ABC≌△ABD,則需要加條件
5、如圖,在△ABC和△ABD中,∠C=∠D=90°,若利用“AAS”證明△ABC≌△ABD,則需要加條件查看答案和解析>>
科目:初中數學 來源: 題型:
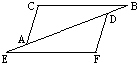 11、如圖,在△ABC和△DEF,AC=DF,AE=BD,當添加條件
11、如圖,在△ABC和△DEF,AC=DF,AE=BD,當添加條件查看答案和解析>>
科目:初中數學 來源: 題型:
 如圖,在△ABC和△ABD中,∠C=∠D=90°,若利用“AAS”證明△ABC≌△ABD,則需要加條件
如圖,在△ABC和△ABD中,∠C=∠D=90°,若利用“AAS”證明△ABC≌△ABD,則需要加條件查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com