如果兩個三角形的兩條邊和其中一邊上的高分別對應相等,那么這兩個三角形的第三條邊所對的角的關系是( )
A.相等
B.不相等
C.相等或互余
D.相等或互補
【答案】
分析:討論:當兩個三角形都是銳角三角形時,AM,DN分別是△ABC和△DEF的高,由BC=EF,AM=DN,AC=DF,易證得Rt△AMC≌RtDNF,則∠BCA=∠DFE;
當兩個三角形都是鈍角三角形時,同樣有兩個三角形的第三條邊所對的角的相等;
當兩個三角形都是直角三角形時,同樣有兩個三角形的第三條邊所對的角的相等且互補;
當兩個三角形一個是鈍角三角形,另一個是銳角三角形時,AM,DN分別是△ABC和△DEF的高,由BC=EF,AM=DN,AC=DF,易證得Rt△AMC≌Rt△DNF,則∠ACM=∠DFN,而∠ACB+∠ACM=180°,即可得到∠ACB+∠DFE=180°.
所以如果兩個三角形的兩條邊和其中一邊上的高分別對應相等,那么這兩個三角形的第三條邊所對的角相等或互補.
解答:解:當兩個三角形都是銳角三角形時,如圖,
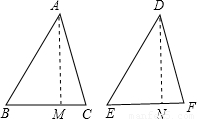
AM,DN分別是△ABC和△DEF的高,
且BC=EF,AM=DN,AC=DF,
在△AMC和R△DNF中,
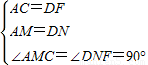
∴△AMC≌△DNF,
∴∠BCA=∠DFE,
即這兩個三角形的第三條邊所對的角的相等;
當兩個三角形都是鈍角三角形時,同樣有兩個三角形的第三條邊所對的角的相等;
當兩個三角形都是直角三角形時,同樣有兩個三角形的第三條邊所對的角的相等且互補;
當兩個三角形一個是鈍角三角形,另一個是銳角三角形時,如圖,AM,DN分別是△ABC和△DEF的高,
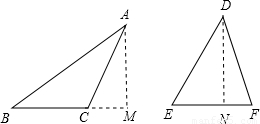
且BC=EF,AM=DN,AC=DF,
易證得Rt△AMC≌Rt△DNF,
∴∠ACM=∠DFN,
而∠ACB+∠ACM=180°,
∴∠ACB+∠DFE=180°,
即這兩個三角形的第三條邊所對的角互補.
所以如果兩個三角形的兩條邊和其中一邊上的高分別對應相等,那么這兩個三角形的第三條邊所對的角相等或互補.
故選D.
點評:本題考查了直角三角形的判定與性質:有兩組邊對應相等兩個直角三角形全等;全等三角形的對應角相等.

 AM,DN分別是△ABC和△DEF的高,
AM,DN分別是△ABC和△DEF的高,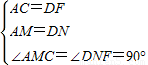



 名校課堂系列答案
名校課堂系列答案