
【題目】如圖,等腰直角![]() 中,
中,![]() ,點
,點![]() 在
在![]() 上,
上,![]() ,連接
,連接![]()
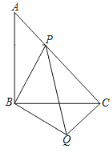
(1)求![]() 的度數;
的度數;
(2)當![]() 時,求
時,求![]() 的長.
的長.
【答案】(1)90°;(2)![]()
【解析】
(1)根據余角的性質得到∠ABP=∠CBQ,根據全等三角形的性質得到∠BCQ=∠A,根據等腰直角三角形的性質即可得到結論;
(2)過P作PD⊥AB于D,得到△ADP是等腰直角三角形,于是得到AD=PD=![]() AP=1,根據勾股定理即可得到結論.
AP=1,根據勾股定理即可得到結論.
解:(1)∵∠ABC=90°,∠PBQ=90°,
∴∠ABP=90°-∠CBP,∠CBQ=90°-∠CBP,
∴∠ABP=∠CBQ,
∵AB=BC,BP=BQ,
∴△ABP≌△CBQ(SAS),
∴∠BCQ=∠A,
∵△ABC是等腰直角三角形,
∴∠A=∠ACB=45°,
∴∠BCQ=45°,
∴∠PCQ=45°+45°=90°;
(2)過P作PD⊥AB于D,
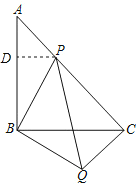
則△ADP是等腰直角三角形,
∴AD=PD=![]() AP=1,
AP=1,
∵AB=4,
∴BD=3,
∴PB=![]() .
.


 快樂小博士鞏固與提高系列答案
快樂小博士鞏固與提高系列答案科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,BA=BC,以AB為直徑的⊙O分別交AC、BC于點D、E,BC的延長線于⊙O的切線AF交于點F.
(1)求證:∠ABC=2∠CAF;
(2)若AC=2![]() ,CE:EB=1:4,求CE的長.
,CE:EB=1:4,求CE的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某公司投入研發費用80萬元![]() 萬元只計入第一年成本
萬元只計入第一年成本![]() ,成功研發出一種產品
,成功研發出一種產品![]() 公司按訂單生產
公司按訂單生產![]() 產量
產量![]() 銷售量
銷售量![]() ,第一年該產品正式投產后,生產成本為6元
,第一年該產品正式投產后,生產成本為6元![]() 件
件![]() 此產品年銷售量
此產品年銷售量![]() 萬件
萬件![]() 與售價
與售價![]() 元
元![]() 件
件![]() 之間滿足函數關系式
之間滿足函數關系式![]() .
.
![]() 求這種產品第一年的利潤
求這種產品第一年的利潤![]() 萬元
萬元![]() 與售價
與售價![]() 元
元![]() 件
件![]() 滿足的函數關系式;
滿足的函數關系式;
![]() 該產品第一年的利潤為20萬元,那么該產品第一年的售價是多少?
該產品第一年的利潤為20萬元,那么該產品第一年的售價是多少?
![]() 第二年,該公司將第一年的利潤20萬元
第二年,該公司將第一年的利潤20萬元![]() 萬元只計入第二年成本
萬元只計入第二年成本![]() 再次投入研發,使產品的生產成本降為5元
再次投入研發,使產品的生產成本降為5元![]() 件
件![]() 為保持市場占有率,公司規定第二年產品售價不超過第一年的售價,另外受產能限制,銷售量無法超過12萬件
為保持市場占有率,公司規定第二年產品售價不超過第一年的售價,另外受產能限制,銷售量無法超過12萬件![]() 請計算該公司第二年的利潤
請計算該公司第二年的利潤![]() 至少為多少萬元.
至少為多少萬元.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】用適當的方法解下列方程:
(1)4(x-1)2=100
(2)x2-2x-15=0
(3)3x2-13x-10=0
(4)3(x-3)2+x(x-3)=0
查看答案和解析>>
科目:初中數學 來源: 題型:
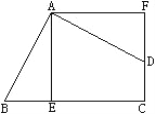
【題目】如圖,四邊形ABCD的∠BAD=∠C=90,AB=AD,AE⊥BC于E,![]() 旋轉后能與
旋轉后能與![]() 重合.
重合.
(1)旋轉中心是哪一點?
(2)旋轉了多少度?
(3)若AE=5㎝,求四邊形AECF的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校計劃成立下列學生社團: A.合唱團: B.英語俱樂部: C.動漫創作社; D.文學社:E.航模工作室為了解同學們對上述學生社團的喜愛情況某課題小組在全校學生中隨機抽取了部分同學,進行“你最喜愛的一個學生社團”的調查,根據調查結果繪制了如下尚不完整的統計圖.
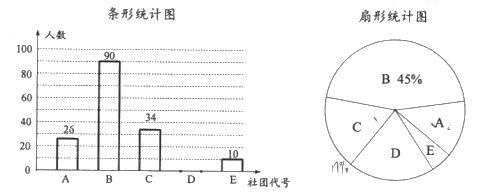
請根據以上信息,解決下列問題:
(1)本次接受調查的學生共有多少人;
(2)補全條形統計圖,扇形統計圖中D選項所對應扇形的圓心角為多少;
(3)若該學校共有學生3000人,估計該學校學生中喜愛合唱團和動漫創作社的總人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,![]() 中,AB=9cm,AC=6cm,兩內角平分線BO和CO相交于點O.
中,AB=9cm,AC=6cm,兩內角平分線BO和CO相交于點O.

(1)若∠A=70,求∠BOC的度數.
(2)若直線DE過點O,與AB、AC分別相交于點D、E,且DE//BC,求![]() 的周長.
的周長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某青春黨支部在精準扶貧活動中,給結對幫扶的貧困家庭贈送甲、乙兩種樹苗讓其栽種.已知乙種樹苗的價格比甲種樹苗貴10元,用480元購買乙種樹苗的棵數恰好與用360元購買甲種樹苗的棵數相同.
(1)求甲、乙兩種樹苗每棵的價格各是多少元?
(2)在實際幫扶中,他們決定再次購買甲、乙兩種樹苗共50棵,此時,甲種樹苗的售價比第一次購買時降低了10%,乙種樹苗的售價不變,如果再次購買兩種樹苗的總費用不超過1500元,那么他們最多可購買多少棵乙種樹苗?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com